时间序列
[时间序列基础参考](https://blog.csdn.net/qq_29831163/article/details/89440215)
# 1、数据介绍
再介绍本篇的内容之前,我们先来看一下本文用到的数据。本文用到的中国银行股票数据下载:[http://pan.baidu.com/s/1gfxRFbH](http://pan.baidu.com/s/1gfxRFbH),提取码d3id。
我们先来导入一下我们的数据,顺便画出收盘价数据的折线图:
```python
import pandas as pd
import matplotlib.pyplot as plt
ChinaBank = pd.read_csv('ChinaBank.csv',index_col = 'Date',parse_dates=['Date'])
#ChinaBank.index = pd.to_datetime(ChinaBank.index)
sub = ChinaBank['2014-01':'2014-06']['Close']
train = sub.ix['2014-01':'2014-03']
test = sub.ix['2014-04':'2014-06']
plt.figure(figsize=(10,10))
print(train)
plt.plot(train)
plt.show()
```
数据如下:
<img src="https://cos.easydoc.net/17082933/files/kes8dn72.png" style="zoom: 35%;" />
介绍了数据,我们接下来进入今天的正题。
---
# 2、时间序列平稳性
## 2.1 平稳性
平稳性就是要求经由样本时间序列所得到的拟合曲线在未来一段时间内仍能顺着现有的形态惯性地延续下去。**平稳性要求序列的均值和方差不发生明显变化**。
**严平稳**
严平稳表示的分布不随时间的改变而改变。
如白噪声(正态),无论怎么取,都是期望为0,方差为1
**弱平稳**
期望与相关系数(依赖性)不变。未来某时刻的$t$的值$x_t$就要依赖于它的过去信息,所以需要依赖性。这种依赖性不能有明显的变化。
## 2.2 差分法
使用**差分法可以使得数据更平稳**,常用的方法就是一阶差分法和二阶差分法。
时间序列差分值的求解可以直接通过pandas中的diff函数得到:
```python
ChinaBank['Close_diff_1'] = ChinaBank['Close'].diff(1)
ChinaBank['Close_diff_2'] = ChinaBank['Close_diff_1'].diff(1)
fig = plt.figure(figsize=(20,6))
ax1 = fig.add_subplot(131)
ax1.plot(ChinaBank['Close'])
ax2 = fig.add_subplot(132)
ax2.plot(ChinaBank['Close_diff_1'])
ax3 = fig.add_subplot(133)
ax3.plot(ChinaBank['Close_diff_2'])
plt.show()
```
绘制的图如下所示:
<img src="https://cos.easydoc.net/17082933/files/kes8h1mi.png" style="zoom: 75%;" />
可以看到,基本上时间序列在一阶差分的时候就已经接近于平稳序列了。
---
# 3、ARIMA模型介绍
## 3.1 自回归模型AR
自回归模型描述当前值与历史值之间的关系,用变量自身的历史时间数据对自身进行预测。自回归模型必须满足平稳性的要求。
自回归模型首先需要确定一个阶数p,表示用几期的历史值来预测当前值。p阶自回归模型的公式定义为:
$y_{t}=\mu+\sum_{i=1}^{p} \gamma_{i} y_{t-i}+\epsilon_{t}$
上式中$y_{t}$是当前值,$u$是常数项,$p$是阶数 $\gamma_{i}$是模型参数(可通过最小二乘法得到),$\epsilon_{t}$是误差。
>**自回归模型有很多的限制:**
>1. 自回归模型是用自身的数据进行预测
>2. 时间序列数据必须具有平稳性
>3. 自回归只适用于预测与自身前期相关的现象
>4. 必须具有相关性,如果相关性小于 0.5 , 则不宜使用
## 3.2 移动平均模型MA
移动平均模型关注的是自回归模型中的误差项的累加,为什么误差能描述模型呢?假设某个值可通过之间前N个值的平均值预测,稍作变化,即实际值可以通过前一值的**预测值加误差**得到.因此实际值可用多个误差值的累加来表示,其形式为:
q阶自回归过程的公式定义如下:$y_{t}=\mu+\epsilon_{t}+\sum_{i=1}^{q} \theta_{i} \epsilon_{t-i}$
移动平均法能有效地消除预测中的随机波动。
## 3.3 自回归移动平均模型ARMA
自回归模型AR和移动平均模型MA模型相结合,我们就得到了自回归移动平均模型ARMA(p,q),计算公式如下:
$y_{t}=\mu+\sum_{i=1}^{p} \gamma_{i} y_{t-i}+\epsilon_{t}+\sum_{i=1}^{q} \theta_{i} \epsilon_{t-i}$
## 3.4 差分自回归移动平均模型ARIMA
将自回归模型、移动平均模型和差分法结合,我们就得到了差分自回归移动平均模型ARIMA(p,d,q),其中d是需要对数据进行差分的阶数。
---
# 4、建立ARIMA模型的过程
一般来说,建立ARIMA模型一般有三个阶段,分别是模型识别和定阶、参数估计和模型检验,接下来,我们一步步来介绍:
## 4.1 模型识别和定阶
模型的识别问题和定阶问题,主要是确定p,d,q三个参数
**参数d的选取**,对于不同d看是否以及平稳:
- (1)直接画出时间序列的趋势图,看趋势判断。
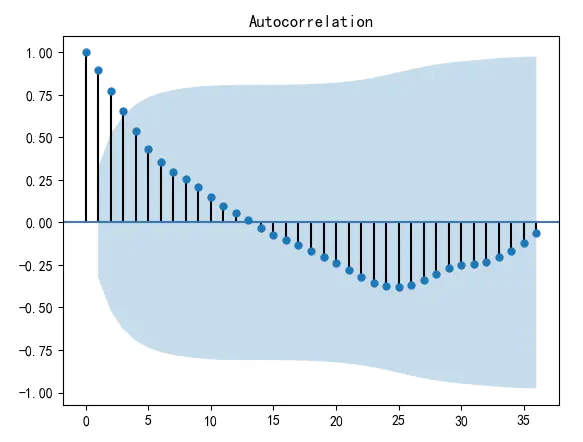
- (2)画自相关和偏自相关图:平稳的序列的自相关图(Autocorrelation)和偏相关图(Partial Correlation)要么拖尾,要么是截尾。
- (3)单位根检验:检验序列中是否存在单位根,如果存在单位根就是非平稳时间序列
- (4)ADF检验(就是结尾示例所使用的)
**参数p、q的选取**
**自相关函数ACF(autocorrelation function)**
自相关函数ACF描述的是时间序列观测值与其过去的观测值之间的线性相关性。计算公式如下:
$A C F(k)=\rho_{k}=\frac{{Cov}\left(y_{t}, y_{t-k}\right)}{{Var}\left(y_{t}\right)}$
其中k代表滞后期数,如果k=2,则代表$y_{t}$和$y_{t-2}$

**偏自相关函数PACF(partial autocorrelation function)**
偏自相关函数PACF描述的是在给定中间观测值的条件下,时间序列观测值预期过去的观测值之间的线性相关性。
举个简单的例子,假设k=3,那么我们描述的是$y_{t}$和$y_{t-3}$之间的相关性,但是这个相关性还受到$y_{t-1}$和$y_{t-2}$的影响。PACF剔除了这个影响,而ACF包含这个影响。
**拖尾和截尾**
拖尾指序列以指数率单调递减或震荡衰减,而截尾指序列从某个时点变得非常小:
<img src="https://cos.easydoc.net/17082933/files/kes8wvm8.png" style="zoom: 75%;" />
出现以下情况,通常视为(偏)自相关系数d阶截尾:
1)在最初的d阶明显大于2倍标准差范围
2)之后几乎95%的(偏)自相关系数都落在2倍标准差范围以内
3)且由非零自相关系数衰减为在零附近小值波动的过程非常突然
<img src="https://cos.easydoc.net/17082933/files/kes8xtlq.png" style="zoom: 75%;" />
出现以下情况,通常视为(偏)自相关系数拖尾:
1)如果有超过5%的样本(偏)自相关系数都落入2倍标准差范围之外
2)或者是由显著非0的(偏)自相关系数衰减为小值波动的过程比较缓慢或非常连续。
<img src="https://cos.easydoc.net/17082933/files/kes8zetx.png" style="zoom: 75%;" />
**p,q阶数的确定**
根据刚才判定截尾和拖尾的准则,p,q的确定基于如下的规则:
<img src="https://cos.easydoc.net/17082933/files/kes902sw.png" style="zoom: 75%;" />
根据不同的截尾和拖尾的情况,我们可以选择AR模型,也可以选择MA模型,当然也可以选择ARIMA模型。接下来,我们就来画一下我们数据的拖尾和截尾情况:
```python
import statsmodels.api as sm
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(train, lags=20,ax=ax1)
ax1.xaxis.set_ticks_position('bottom')
fig.tight_layout()
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(train, lags=20, ax=ax2)
ax2.xaxis.set_ticks_position('bottom')
fig.tight_layout()
plt.show()
```
结果如下:
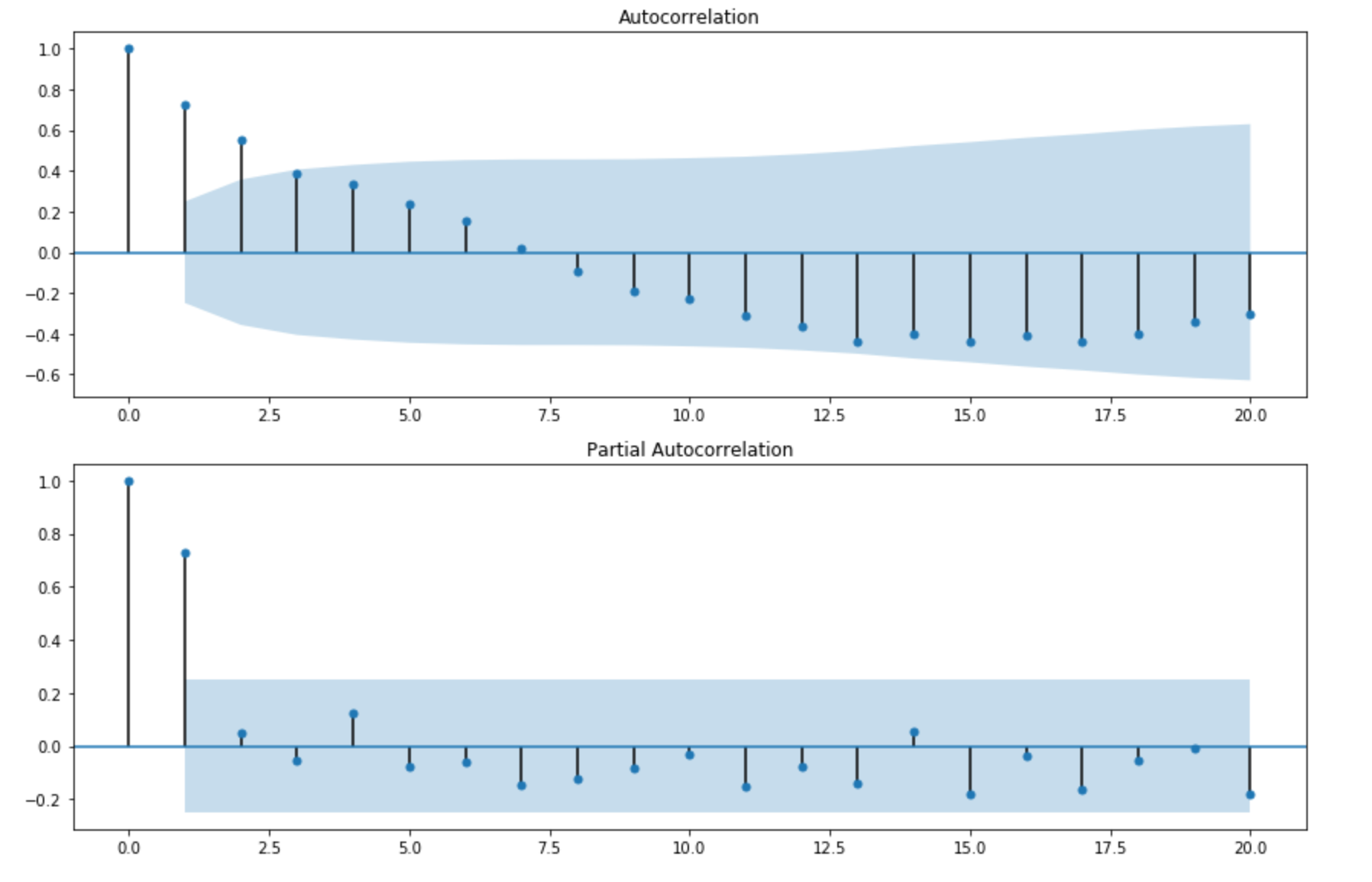
**关于AR,MA,ARMA等模型应该怎么选**
要注意对于这几个模型的选择绝对不是IC谁高就选谁。正确的流程:根据acf和pacf的特点进行选择。比如咱们的图自相关系数4阶拖尾,偏自相关系数2阶截尾,这样对应的model是AR(2),又或者说ARIMA(2,d,0)
但是如果**p q都不为0**,那么ACF和PACF图**均为拖尾**表现,p、q的值就无法一眼看出来了。**解决方法**:从最低阶开始拟合模型,遍历参数并观察拟合结果的变化。
又或者直接使用**使用auto.arima()函数,自动获取最佳的ARIMA模型参数**(其实就是利用AIC、BIC准则(如下)循环寻找最佳参数),见:[用ARIMA模型做需求预测](https://www.jianshu.com/p/f547bb4b50c3)
**注**:对于平稳的时间序列,理想情形是自相关函数在一定的条件下服从**正态分布**,当样本量n很大时,ACF落在区间[-1.96/sqrt(n), +1.96/sqrt(n)]的概率为95%,若超过这个线,则表示位于5%是异常的。最后,如果ACF和PACF迅速衰减至这两条线之间并做小幅震荡,就可以认为是截尾的了。
## 4.2 参数估计
通过拖尾和截尾对模型进行定阶的方法,往往具有很强的主观性。回想我们之前在参数预估的时候往往是怎么做的,不就是损失和正则项的加权么?我们这里能不能结合最终的预测误差来确定p,q的阶数呢?在相同的预测误差情况下,根据奥斯卡姆剃刀准则,模型越小是越好的。那么,平衡预测误差和参数个数,我们可以根据信息准则函数法,来确定模型的阶数。预测误差通常用平方误差即残差平方和来表示。
常用的信息准则函数法有下面几种:
**AIC准则**
AIC准则全称为全称是最小化信息量准则(Akaike Information Criterion),计算公式如下:
AIC = =2 *(模型参数的个数)-2ln(模型的极大似然函数)
**BIC准则**
AIC准则存在一定的不足之处。当样本容量很大时,在AIC准则中拟合误差提供的信息就要受到样本容量的放大,而参数个数的惩罚因子却和样本容量没关系(一直是2),因此当样本容量很大时,使用AIC准则选择的模型不收敛与真实模型,它通常比真实模型所含的未知参数个数要多。BIC(Bayesian InformationCriterion)贝叶斯信息准则弥补了AIC的不足,计算公式如下:
BIC = ln(n) * (模型中参数的个数) - 2ln(模型的极大似然函数值),n是样本容量
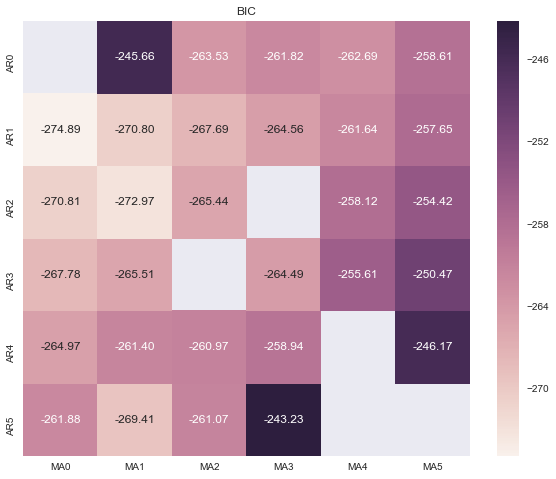
好了,我们通过类似于网格搜索的方式来寻找我们模型最佳的p,q组合吧,这里我们使用BIC进行试验,AIC同理:
```python
#遍历,寻找适宜的参数
import itertools
import numpy as np
import seaborn as sns
p_min = 0
d_min = 0
q_min = 0
p_max = 5
d_max = 0
q_max = 5
# Initialize a DataFrame to store the results,,以BIC准则
results_bic = pd.DataFrame(index=['AR{}'.format(i) for i in range(p_min,p_max+1)],
columns=['MA{}'.format(i) for i in range(q_min,q_max+1)])
for p,d,q in itertools.product(range(p_min,p_max+1),
range(d_min,d_max+1),
range(q_min,q_max+1)):
if p==0 and d==0 and q==0:
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = np.nan
continue
try:
model = sm.tsa.ARIMA(train, order=(p, d, q),
#enforce_stationarity=False,
#enforce_invertibility=False,
)
results = model.fit()
results_bic.loc['AR{}'.format(p), 'MA{}'.format(q)] = results.bic
except:
continue
results_bic = results_bic[results_bic.columns].astype(float)
fig, ax = plt.subplots(figsize=(10, 8))
ax = sns.heatmap(results_bic,
mask=results_bic.isnull(),
ax=ax,
annot=True,
fmt='.2f',
)
ax.set_title('BIC')
plt.show()
```
绘制的热力图如下:
我们上面采用了循环的方式,其实可以用更简单的方法得到p和q的最优值:
```python
train_results = sm.tsa.arma_order_select_ic(train, ic=['aic', 'bic'], trend='nc', max_ar=8, max_ma=8)
print('AIC', train_results.aic_min_order)
print('BIC', train_results.bic_min_order)
```
结果为:
```python
AIC (1, 0)
BIC (1, 0)
```
表明我们应该选择AR(1)模型。
一般来说,BIC准则得到的ARMA模型的阶数较AIC的低。
## 4.3 模型检验
这里的模型检验主要有两个:
1)**检验残差的正态性**
2)**检验残差序列的随机性,即残差之间是独立的**
### 4.31残差检验
>**主要针对残差进行正态性检验和自相关性检验**。
残差满足正态性,主要是为了残差集中于某一个数值,如果该值与0很接近,则它实际服从均值为0的正态分布,即它是一个白噪声。白噪声是指功率谱密度在整个频域内均匀分布的噪声。白噪声或白杂讯,是一种功率频谱密度为常数的随机信号或随机过程。换句话说,此信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。
>
>残差满足非自相关性,主要是为了在残差中不再包括AR或者MA过程产生的序列。正态性检验可以使用shapiro.test函数来检查,当p-value>0.05时表明满足正态分布,该值越大越好,直到接近于1.残差的自相关性可以用函数tsdiag(model)来迅速检验。该函数会列出残差的散点图,自相关性acf检验和Box.test的检验值(pvalue大于0.05即满足非自相关性)。
**为什么残差要是白噪声?
答:得到白噪声序列,就说明时间序列中有用的信息已经被提取完毕了,剩下的全是随机扰动,是无法预测和使用的,残差序列如果通过了白噪声检验,则建模就可以终止了,因为没有信息可以继续提取。如果残差不是白噪声,就说明残差中还有有用的信息,需要修改模型或者进一步提取。**
```python
resid = model_results.resid #赋值
fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2)
plt.show()
```
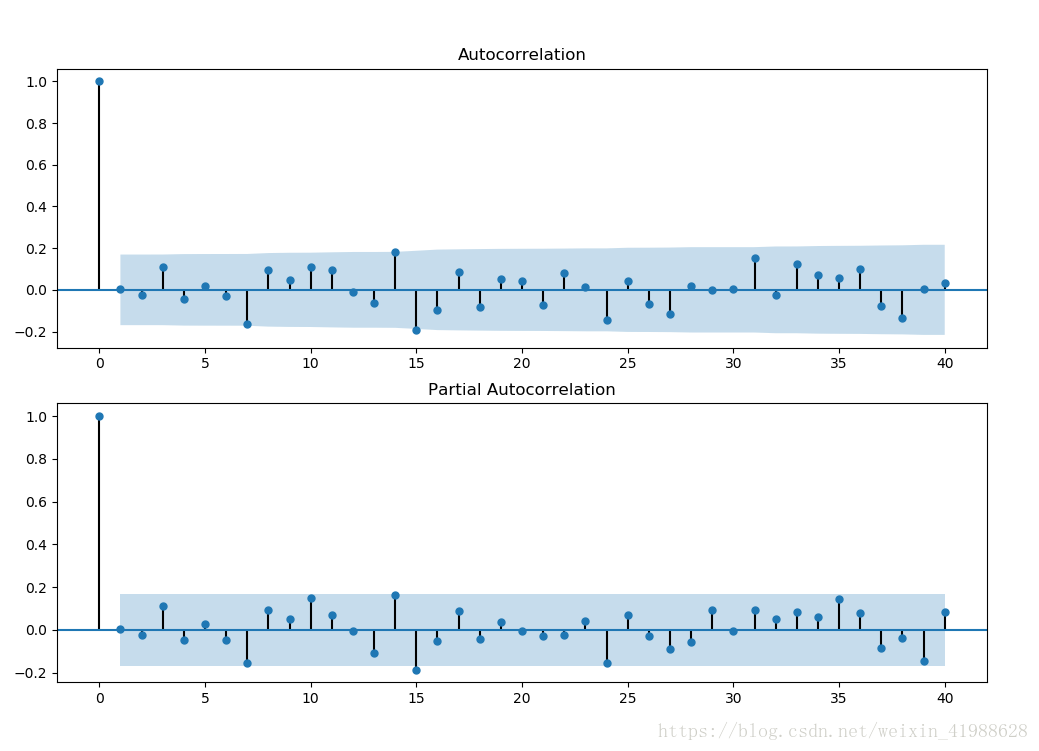
### 4.32做D-W检验
德宾-沃森(Durbin-Watson)检验。德宾-沃森检验,简称D-W检验,是目前检验自相关性最常用的方法,但它只使用于检验一阶自相关性。因为自相关系数ρ的值介于-1和1之间,所以 0≤DW≤4。
DW=O=>ρ=1 即存在正自相关性
DW=4<=>ρ=-1 即存在负自相关性
DW=2<=>ρ=0 即不存在(一阶)自相关性
因此,当DW值显著的接近于O或4时,则存在自相关性,而接近于2时,则不存在(一阶)自相关性。这样只要知道DW统计量的概率分布,在给定的显著水平下,根据临界值的位置就可以对原假设H0进行检验。
```python
print(sm.stats.durbin_watson(model_results.resid.values))
```
结果:
### 4.33观察是否符合正态分布
各种办法
### 4.346 Ljung-Box检验(白噪声检验)
Ljung-Box test是对randomness的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验,我们常常采用的方法还包括计算ACF和PCAF并观察其图像,但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数,判断序列总体的相关性或者说随机性是否存在。
时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型,其残差被假定为高斯白噪声序列,所以当我们用ARIMA模型去拟合数据时,拟合后我们要对残差的估计序列进行LB检验,判断其是否是高斯白噪声,如果不是,那么就说明ARIMA模型也许并不是一个适合样本的模型。
```python
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
data = np.c_[range(1,41), r[1:], q, p]
table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))
```
结果:
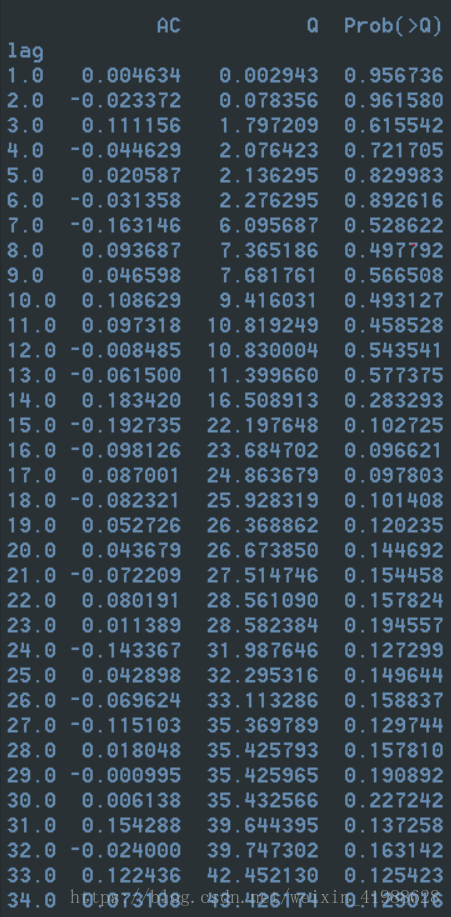
结果分析:原假设为白噪声(相关系数为零)检验的结果就是看最后一列前十二行的检验概率(一般观察滞后1~12阶),如果检验概率小于给定的显著性水平,比如0.05、0.10等就拒绝原假设,即为非白噪声。
就结果来看,如果取显著性水平为0.05或者0.1,结果不小于显著性水平,那么相关系数与零没有显著差异,即为白噪声序列。
## 4.4 模型预测
预测主要有两个函数,一个是predict函数,一个是forecast函数,predict中进行预测的时间段必须在我们训练ARIMA模型的数据中,forecast则是对训练数据集末尾下一个时间段的值进行预估。
```python
model = sm.tsa.ARIMA(sub, order=(1, 0, 0))
results = model.fit()
predict_sunspots = results.predict(start=str('2014-04'),end=str('2014-05'),dynamic=False)
print(predict_sunspots)
fig, ax = plt.subplots(figsize=(12, 8))
ax = sub.plot(ax=ax)
predict_sunspots.plot(ax=ax)
plt.show()
```
结果如下:
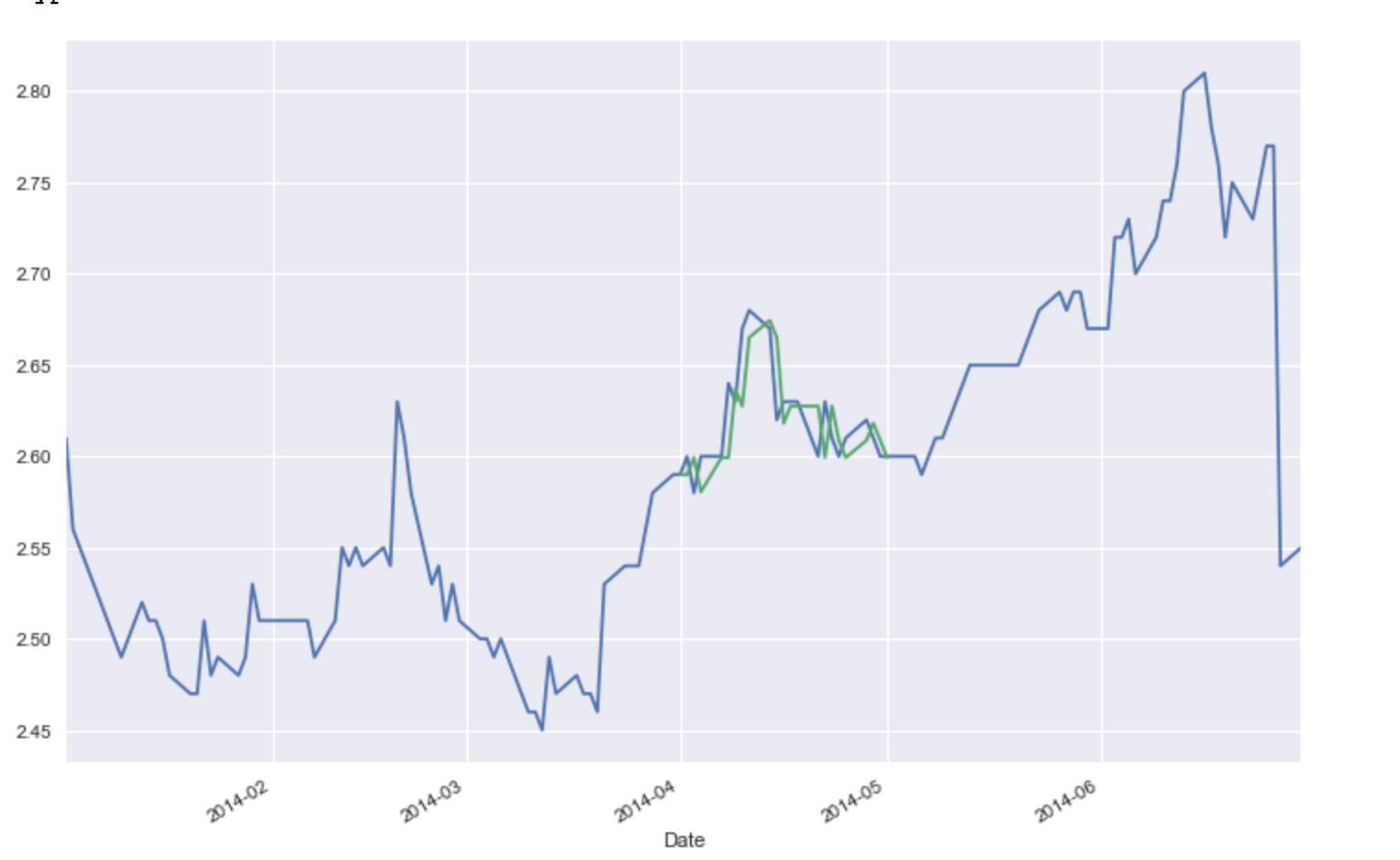
预估下一个值:
```python
results.forecast()[0]
```
# 5、示例:使用ARIMA 模型对某餐厅的销售数据进行预测
使用ARIMA 模型对非平稳时间序列进行建模操作
差分运算具有强大的确定性的信息提取能力, 许多非平稳的序列差分后显示出平稳序列的性质, 这是称这个非平稳序列为差分平稳序列。
对差分平稳序列可以还是要ARMA 模型进行拟合, ARIMA 模型的实质就是差分预算与 ARMA 模型的结合
```python
#coding=gbk
#使用ARIMA 模型对非平稳时间序列记性建模操作
#差分运算具有强大的确定性的信息提取能力, 许多非平稳的序列差分后显示出平稳序列的性质, 这是称这个非平稳序列为差分平稳序列。
#对差分平稳序列可以还是要ARMA 模型进行拟合, ARIMA 模型的实质就是差分预算与 ARMA 模型的结合。
#导入数据
import pandas as pd
filename = r'D:\datasets\arima_data.xls'
data = pd.read_excel(filename, index_col = u'日期')
#画出时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #定义使其正常显示中文字体黑体
plt.rcParams['axes.unicode_minus'] = False #用来正常显示表示负号
# data.plot()
# plt.show()
```
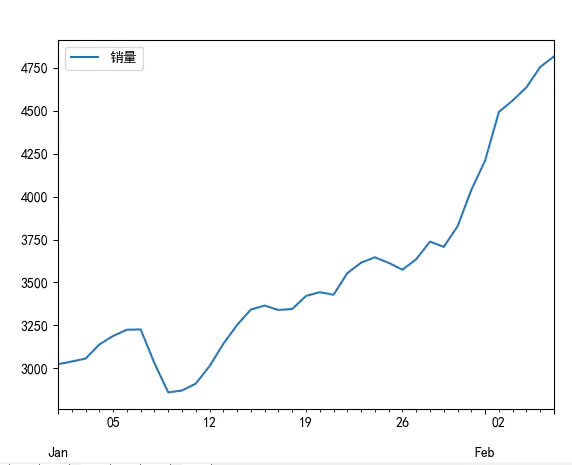
```python
#画出自相关性图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
# plot_acf(data)
# plt.show()
#平稳性检测
from statsmodels.tsa.stattools import adfuller
print('原始序列的检验结果为:',adfuller(data[u'销量']))
#原始序列的检验结果为: (1.8137710150945268, 0.9983759421514264, 10, 26, {'1%': -3.7112123008648155,
# '10%': -2.6300945562130176, '5%': -2.981246804733728}, 299.46989866024177)
#返回值依次为:adf, pvalue p值, usedlag, nobs, critical values临界值 , icbest, regresults, resstore
#adf 分别大于3中不同检验水平的3个临界值,单位检测统计量对应的p 值显著大于 0.05 , 说明序列可以判定为 非平稳序列
```
```python
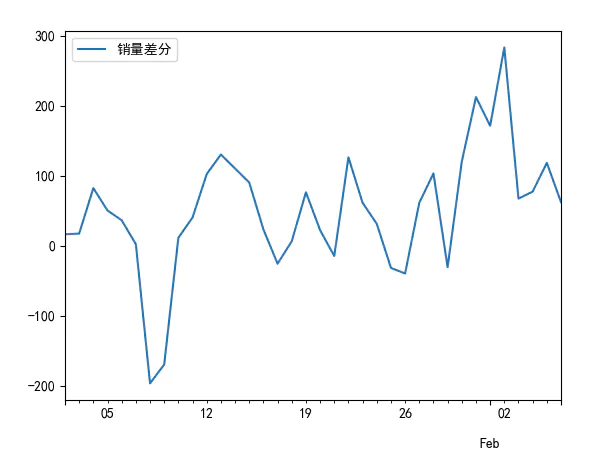
#对数据进行差分后得到 自相关图和 偏相关图
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #画出差分后的时序图
# plt.show()
plot_acf(D_data) #画出自相关图
# plt.show()
plot_pacf(D_data) #画出偏相关图
# plt.show()
print(u'差分序列的ADF 检验结果为: ', adfuller(D_data[u'销量差分'])) #平稳性检验
#差分序列的ADF 检验结果为: (-3.1560562366723537, 0.022673435440048798, 0, 35, {'1%': -3.6327426647230316,
# '10%': -2.6130173469387756, '5%': -2.9485102040816327}, 287.5909090780334)
#一阶差分后的序列的时序图在均值附近比较平稳的波动, 自相关性有很强的短期相关性, 单位根检验 p值小于 0.05 ,所以说一阶差分后的序列是平稳序列
```
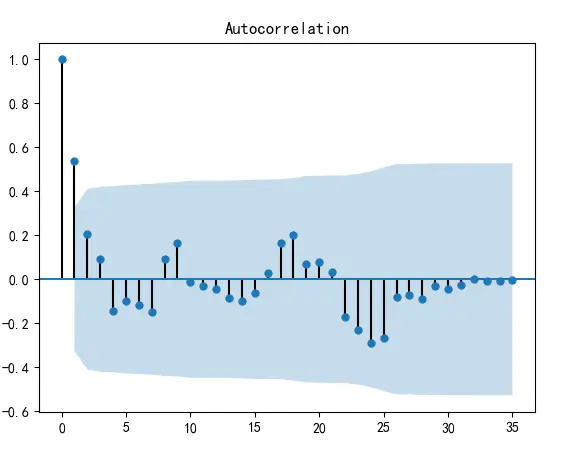
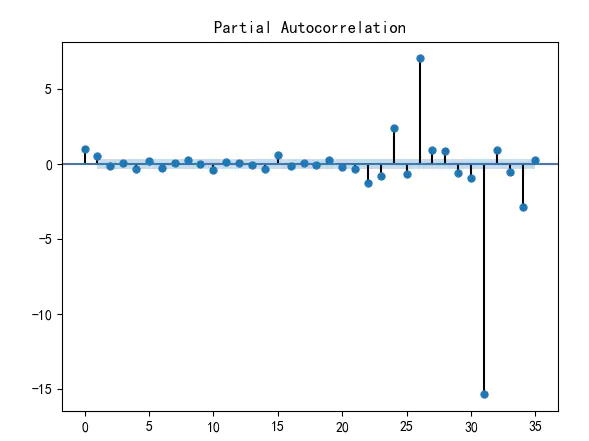
```python
#对一阶差分后的序列做白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果:',acorr_ljungbox(D_data, lags= 1)) #返回统计量和 p 值
# 差分序列的白噪声检验结果: (array([11.30402222]), array([0.00077339])) p值为第二项, 远小于 0.05
#如果一个序列是平稳的,那么下面我们就要判断数据是否是白噪声,白噪声没有研究的意义(https://zhuanlan.zhihu.com/p/26227700)
#对模型进行定阶
from statsmodels.tsa.arima_model import ARIMA
pmax = int(len(D_data) / 10) #一般阶数不超过 length /10
qmax = int(len(D_data) / 10)
bic_matrix = []
for p in range(pmax +1):
temp= []
for q in range(qmax+1):
try:
temp.append(ARIMA(data, (p, 1, q)).fit().bic)
except:
temp.append(None)
bic_matrix.append(temp)
bic_matrix = pd.DataFrame(bic_matrix) #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin() #先使用stack 展平, 然后使用 idxmin 找出最小值的位置
print(u'BIC 最小的p值 和 q 值:%s,%s' %(p,q)) # BIC 最小的p值 和 q 值:0,1
#所以可以建立ARIMA 模型,ARIMA(0,1,1)
model = ARIMA(data, (p,1,q)).fit()
model.summary2() #生成一份模型报告
model.forecast(5) #为未来5天进行预测, 返回预测结果, 标准误差, 和置信区间
```
示例来源:[时间序列模式(ARIMA)---Python实现](https://juejin.im/post/6844904135737737230#heading-7)
---
解说视频:[B站:机器学习经典算法:时间序列ARIMA模型](https://www.bilibili.com/video/BV1F441187xt?p=1)
参考文献:
[ARIMA模型原理及实现](https://blog.csdn.net/sunnyxidian/article/details/92946542)
[机器学习(五)——时间序列ARIMA模型](https://blog.csdn.net/weixin_41988628/article/details/83149849)
[时间序列模型 一到七](https://blog.csdn.net/qq_29831163/article/details/89440215)