初中上数学组卷
# 2020年02月24日康少的初中上数学组卷
## 一.选择题(共1小题)
1.近似数35.04万精确到( )
A.百位
B.百分位
C.万位
D.个位
## 二.填空题(共2小题)
2.若|a|+|b|=2,则满足条件的整数a、b的值有(——)组.
3.如图,若数轴上a的绝对值是b的绝对值的3倍,则数轴的原点在点(——)或点(——).(填“A”、“B”“C”或“D”)

## 三.解答题(共37小题)
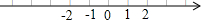
4.操作探究:已知在纸面上有一数轴(如图所示),
操作一:
(1)折叠纸面,使表示的1点与-1表示的点重合,则-3表示的点与(——)表示的点重合;
操作二:
(2)折叠纸面,使-1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数(——)表示的点重合;
②若数轴上A、B两点之间距离为11,(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少.
5.小明早晨跑步,他从自家向东跑了2千米到达小彬家,继续向东跑了1.5千米到达小红家,然后向西跑了4.5千米到达中心广场,最后回到家.
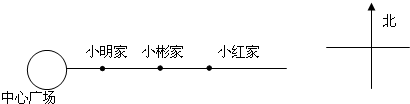
(1)以小明家为原点,以向东的方向为正方向,用1 个单位长度表示1千米,你能在数轴上表示出中心广场,小彬家和小红家的位置吗?
(2)小彬家距中心广场多远?
(3)小明一共跑了多少千米?
6.【概念学习】
规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③,读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④,读作“-3的圈4次方”,一般地,把$\dfrac{a}{1}$)⑤=(——);
(2)关于除方,下列说法错误的是(——)
A.任何非零数的圈2次方都等于1;
B.对于任何正整数n,1ⓝ=1;
C.3④=4③;
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
【深入思考】
我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
(1)试一试:仿照上面的算式,将下列运算结果直接写成幂的形式.
(-3)④=(——);5⑥=(——);($-\dfrac{1}{2}$)⑩=(——).
(2)想一想:将一个非零有理数a的圈n次方写成幂的形式等于(——);
(3)算一算:122÷($-\dfrac{1}{3}$)④×(-2)⑤-($-\dfrac{1}{3}$)⑥÷33.
7.某茶叶加工厂一周生产任务为182kg,计划平均每天生产26kg,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
+3,-2,-4,+1,-1,+6,-5
(1)这一周的实际产量是多少kg?
(2)若该厂工人工资实际计件工资制,按计划每生产1kg茶叶50元,每超产1kg奖10元,每天少生产1kg扣10元,那么该厂工人这一周的工资总额是多少?
8.已知在纸面上有一数轴(如图),折叠纸面.例如:若数轴上数2表示的点与数-2表示的点重合,则数轴上数-4表示的点与数4表示的点重合,根据你对例题的理解,解答下列问题:
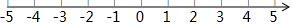
若数轴上数-3表示的点与数1表示的点重合.(根据此情境解决下列问题)
①则数轴上数3表示的点与数(——)表示的点重合.
②若点A到原点的距离是5个单位长度,并且A、B两点经折叠后重合,则B点表示的数是(——).
③若数轴上M、N两点之间的距离为2018,并且M、N两点经折叠后重合,如果M点表示的数比N点表示的数大,则M点表示的数是(——).则N点表示的数是(——).

9.先阅读,后探究相关的问题
【阅读】|5-2|表示5与2差的绝对值,也可理解为5与2两数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两数在数轴上所对应的两点之间的距离.
(1)如图,先在数轴上画出表示点2.5的相反数的点B,再把点A向左移动1.5个单位,得到点C,则点B和点C表示的数分别为(——)和(——),B,C两点间的距离是(——);
(2)数轴上表示x和-1的两点A和B之间的距离表示为(——);如果|AB|=3,那么x为(——);
(3)若点A表示的整数为x,则当x为(——)时,|x+4|与|x-2|的值相等;
(4)要使代数式|x+5|+|x-2|取最小值时,相应的x的取值范围是(——).

10.如图,A,B分别为数轴上的两点,点A对应的数是-2,点B对应的数是10.现有点P从点A出发,以4个单位长度/秒的速度向右运动,同时另一点Q从点B出发,以1个单位长度/秒的速度向右运动,设运动时间为t秒.
(1)A、B两点之间的距离为(——);
(2)当t=1时,P、B两点之间的距离为(——);
(3)在运动过程中,线段PB、BQ、PQ中是否会有两条线段相等?若有,请求出此时t的值;若没有,请说明理由.
11.实数a,b,c在数轴上的位置如图,化简|b+c|-|b+a|+|a+c|.

12.列方程解应用题
某服装厂生产一种裤子和T恤,裤子每件定价100元,T恤每件定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案,方案一:买一件裤子送一件T恤;方案二:裤子和T恤都按定价的80%付款.现某客户要到该服装厂购买裤子30件,T恤x件(x>30).
(1)按方案一,购买裤子和T恤共需付款(——)元(用含x的式子表示);按方案二,购买裤子和T恤共需付款(——)元(用含x的式子表示);
(2)计算一下,购买多少件T恤时,两种优惠方案付款一样?
(3)若两种优惠方案可同时使用,当x=40时,你能给出一种更为省钱的购买方案吗?若能,请写出你的购买方案,并说明理由.
13.已知点A、B在数轴上表示的数分别为m、n.
(1)填写下表:
| m | 5 | -5 | -7 | -7 |
| -------------- | ---- | ---- | ---- | ---- |
| n | 3 | 0 | 3 | -3 |
| A、B两点的距离 | (——) | (——) | (——) | (——) |
(2)若A、B两点的距离为d,则d=(——).(用含m,n的式子表示)
(3)由(2)的结论可知:|x-2|的意义是:数轴上表示数x的点到表示(——) 的点的距离.
(4)若动点C表示的数为x,则|x-2|+|x+3|的最小值是(——).
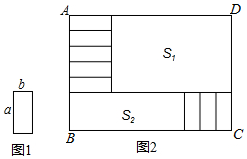
14.将8张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b,AD=30.
(1)当a=8,b=3时,长方形ABCD的面积(——).
(2)S1-S2的值(用含a,b的式子表示).
15.康乐公司在A、B两地分别有同型号的机器17台和15台,现要运往甲地18台,乙地14台.从A、B两地运往甲、乙两地的费用如下表:
| 甲地(元/台) | 乙地(元/台) |
| ---------------------------------------------------------------------------------------------------------------------- | ------------- | ------------- |
| A地 | 600 | 500 |
| B地 | 400 | 800 |
从A地运往甲地x台,总费用多少元?(用含x的代数式表示)
16.甲、乙、丙三家超市销售同一品牌书包,标价均为x元/个.甲超市先降价20%,再提价10%销售;乙超市先提价10%,再降价20%销售;丙超市降价10%销售.三家超市的书包销售价各是多少,你会选择哪家超市购物?
17.已知a、b互为相反数,c、d互为倒数,m的绝对值是5,n是最大的负整数,求代数式2011(a+b)-4cd+2mn的值.
18.移动公司有多种手机入网收费方式,其中甲、乙两种方式分别是:
甲种:(普通型)每分钟通话费0.6元.
乙种:(大众型)月租费20元,外加每分钟通话费0.2元.
①如果某月通话时间为x分钟,则两种方式下应该支付的费用分别为:
W甲=(——)元,W乙=(——)元.
②如果王老师平均每月手机通话80分钟,你认为王老师采用哪种方式较为合算?
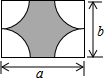
19.已知长方形的长为a,宽为b,空白部分为$\dfrac{1}{4}$半圆.
(1)求阴影部分的面积.(用a、b字母表示)
(2)当a=3,b=1时,求阴影部分的面积.(结果用π表示)
20.已知a与b互为相反数,c与d互为倒数,e为绝对值最小的数,求式子2004(a+b)+cd+e的值.

21.如图,正方形ABCD的周长为40米,甲、乙两人分别从A、B同时出发,沿正方形的边行走,甲按逆时针方向每分钟行55米,乙按顺时针方向每分钟行30米.
(1)出发后(——)分钟时,甲乙两人第一次在正方形的顶点处相遇;
(2)如果用记号(a,b)表示两人行了a分钟,并相遇过b次,那么当两人出发后第一次处在正方形的两个相对顶点位置时,对应的记号应是(——).
22.为庆祝“六一”儿童节,某市中小学统一组织文艺汇演,甲、乙两所学校共92人(其中甲校的人数多于乙校的人数,且甲校的人数不足90人)准备统一购买服装参加演出;下面是某服装厂给出的演出服装的价格表
| 购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
| ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ | --------- | ---------- | -------- |
| 每套服装的价格 | 60元 | 50元 | 40元 |
(1)如果两所学校分别单独购买服装一共应付5000元,甲、乙两所学校各有多少学生准备参加演出?
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出,请你为两所学校设计一种最省钱的购买服装方案.
23.A、B两地相距64千米,甲从A地出发,每小时行14千米,乙从B地出发,每小时行18千米.
(1)若两人同时出发相向而行,则需经过几小时两人相遇?
(2)若两人同时出发相向而行,则需几小时两人相距16千米?
(3)若甲在前,乙在后,两人同时同向而行,则几小时后乙超过甲10千米?
24.A、B两地相距120km,一辆汽车以每小时50km的速度从A地出发,另一辆货车以每小时40km的速度从B地出发,两车相向而行.经过多少时间两车相距30km?
25.从2004年8月1日起,浙江省城乡居民生活用电执行新的电价政策,小聪家今年安装了新的电表,他了解到安装”一户一表”的居民用户,按用抄见电量(每家用户电表所表示的用电量)实行阶梯式累进加价,其中低于50千瓦时(含50千瓦时)部分电价不调整;51-200千瓦时部分每千瓦时电价上调0.03元;超过200千瓦时的部分每千瓦时电价再上调0.10元.已知调整前电价统一为每千瓦时0.53元.
(1)若小聪家10月份的用电量为130千瓦时,则10月份小聪家应付电费多少元?
(2)已知小聪家10月份的用电量为m千瓦时,请完成下列填空:
①若m≤50千瓦时,则10月份小聪家应付电费为(——)元;
②若50<m≤200千瓦时,则10月份小聪家应付电费为(——)元;
③若m>200千瓦时,则10月份小聪家应付电费为(——)元.
(3)若10月份小聪家应付电费为96.50元,则10月份小聪家的用电量是多少千瓦时?
26.我们规定:若关于x的一元一次方程ax=b的解为b+a,则称该方程为“和解方程”. 例如:方程2x=-4的解为x=-2,而-2=-4+2,则方程2x=-4为“和解方程”.
请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程3x=m是“和解方程”,求m的值;
(2)已知关于x的一元一次方程-2x=mn+n是“和解方程”,并且它的解是x=n,求m,n的值.
27.牧场上的草长得一样地密,一样地快.已知70头牛在24天里把草吃完,而30头牛就可吃60天.如果要吃96天,问牛数该是多少?
28.某工人计划加工一批产品,如果每小时加工产品10个,就可以在预定时间完成任务,如果每小时多加工2个,就可以提前1小时完成任务.
(1)该产品的预定加工时间为几小时?
(2)若该产品销售时的标价为100元/个,按标价的八折销售时,每个仍可以盈利25元,该批产品总成本为多少元?
29.A、B两列火车长分别是120m和144m,A车比B车每秒多行5m.
(1)两列相向行驶,从相遇到两车全部错开需8秒,问两车的速度各是多少?
(2)在(1)的条件下,若同向行驶,A车的车头从B车的车尾追及到A车全部超出B车,需要多少秒?
30.环行跑道周长为400米,甲乙两人在同时同地顺时针沿环行跑道跑,甲每分钟跑52米,乙每分钟跑46米,甲乙两人每跑100米休息1分钟,问甲何时追上乙?
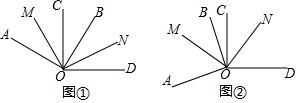
31.如图①,∠AOB=∠COD=90°,OM平分∠AOC,ON平分∠BOD.
(1)已知∠BOC=20°,且∠AOD小于平角,求∠MON的度数;
(2)若(1)中∠BOC=α,其它条件不变,求∠MON的度数;
(3)如图②,若∠BOC=α,且∠AOD大于平角,其它条件不变,求∠MON的度数.
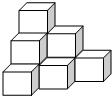
32.棱长为a的正方体,摆成如图所示的形状.
(1)如果这一物体摆放三层,试求该物体的表面积;
(2)依图中摆放方法类推,如果该物体摆放了上下20层,求该物体的表面积.
(3)依图中摆放方法类推,如果该物体摆放了上下n层,求该物体的表面积.
33.图1是由一副三角板拼成的图案,根据图中提供的信息,解答下列问题:
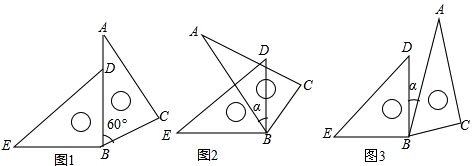
(1)图1中,∠EBC的度数为(——);
(2)能否将图1中的三角板ABC绕点B逆时针旋转α度(0°<α<90°,如图2),使旋转后的∠ABE=2∠DBC?若能,求出α的度数,若不能,请说明理由;
(3)能否将图1中的三角板ABC绕点B顺时针旋转α度(0°<α<90°,如图3),使旋转后的∠ABE=2∠DBC?请直接回答,不必说明理由;
答:(——)(填“能”或“不能”)
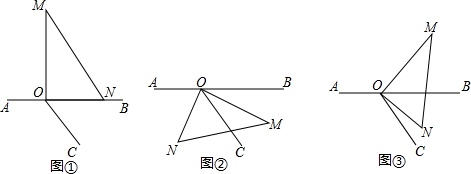
34.如图①,点O为直线AB上一点,过点O作射线OC,将一直角三角板如图摆放(∠MON=90°).
(1)将图①中的三角板绕点O旋转一定的角度得图②,使边OM恰好平分∠BOC,问:ON是否平分∠AOC?请说明理由;
(2)将图①中的三角板绕点O旋转一定的角度得图③,使边ON在∠BOC的内部,如果∠BOC=60°,则∠BOM与∠NOC之间存在怎样的数量关系?请说明理由.
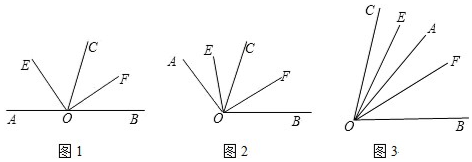
35.下列各小题中,都有OE平分∠AOC,OF平分∠BOC.
(1)如图①,若点A、O、B在一条直线上,∠EOF=(——);
(2)如图②,若点A、O、B不在一条直线上,∠AOB=140°,则∠EOF=(——);
(3)由以上两个问题发现:当∠AOC在∠BOC的外部时,∠EOF与∠AOB的数量关系是∠EOF=(——);
(4)如图③,若OA在∠BOC的内部,∠AOB和∠EOF还存在上述的数量关系吗;请简单说明理由;
36.如图,已知∠AOC=70°,∠BOD=100°,∠AOB是∠DOC的3倍,求∠AOB的度数.

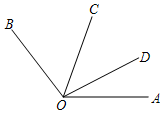
37.如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC=(——)°,∠DOE=(——)°;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC=(——)°,∠DOE=(——)°;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.
38.如果一个棱柱一共有12顶点,底边长是侧棱长的一半,并且所有的棱长的和是120cm,求每条侧棱的长.
39.如图,点C在线段AB上,AC=6cm,MB=10cm,点M、N分别为AC、BC的中点.
(1)求线段BC、MN的长;
(2)若C在线段AB的延长线上,且满足AC-BC=6cm,M、N分别是线段AC、BC的中点,求MN的长度.

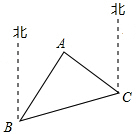
40.如图,A点在B处的北偏东40°方向,C点在B处的北偏东85°方向,A点在C处的北偏西45°方向,求∠BCA及∠BAC的度数.