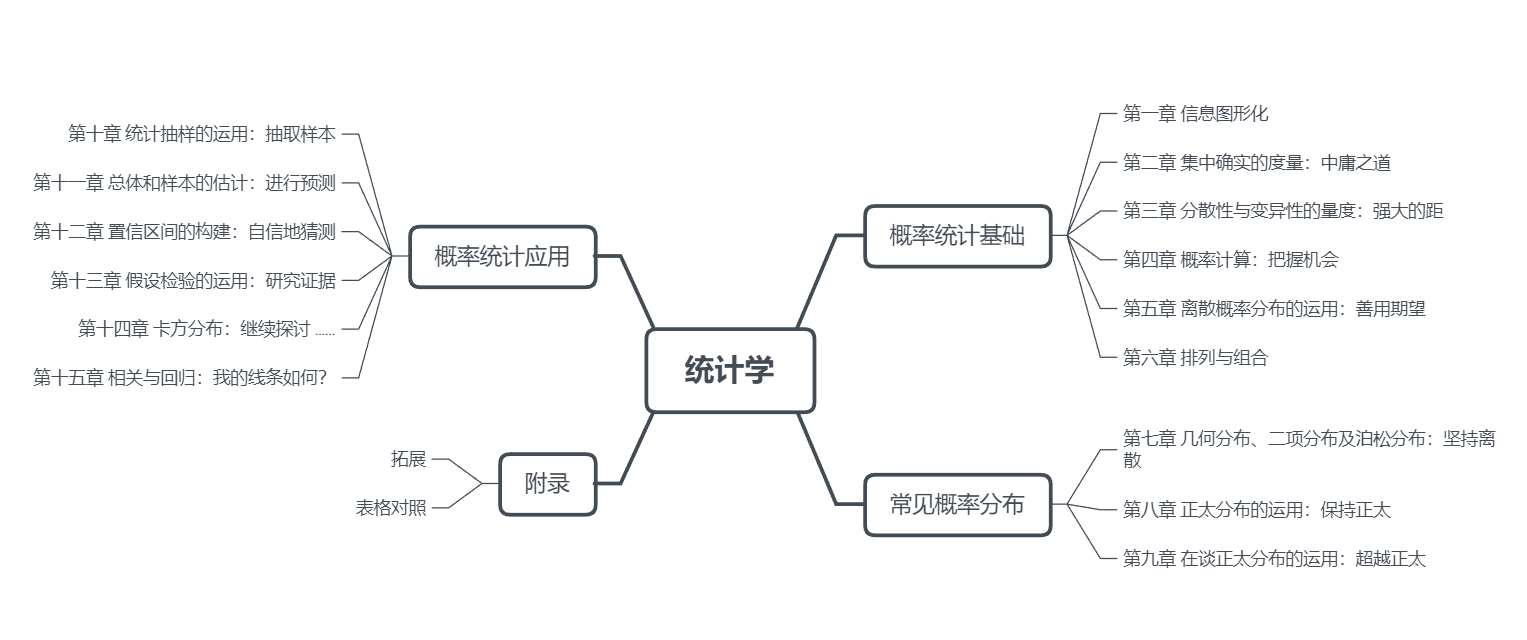
概率论基础
::: hljs-center
:::
# 第一章 可视化
**1. 垂直柱形图和横向柱形图的区别在于:**
- 当文本过长时,一般采用横向
- 垂直柱形图表示频率,横向表示百分比
**2. 定性指标与定量指标**
- 定性指标:不能转化成数字表示,一般是一种分类
- 定量指标:可以转化后数字
**3. 直方图的柱子之间必须是没有间隙的,而且宽度一样**
# 第二章 集中趋势的度量
**1. 均值的专用符号:U(miu)**
**2. 处理频数:**
**3. 异常值会导致偏斜(要么抬高均值,要么拉低均值)**
**4. 当偏斜数据和异常值使均值产生误导时,我们需要用到中位数。**
**5. 当数值呈现两极化的时候(比如:游泳班孩子和家长的年龄),众数就派上了用场**
**6. 众数是唯一能用于类别数据的平均数。**
**7. 均值,中位数,众数区别**。
**总结: 均值,中位数和众数都是平均数,平均数主要用在寻找数据集典型值。**
# 第三章 分散性与变异性的量度
- **全距** = 最大值 - 最小值; 它仅仅描述了**数据的宽度**;
- **四分位距** = 上四分位距 - 下四分位距(作用:**用于排除异常值**)
- **箱线图**:用来显示各种距的图;如果你的数据中有异常值,全距会很宽。通过观察箱型图上的线,就能了解数据的**偏斜程度**。
- **方差**:量度**数据分散情况**; 公式:$\frac{\sum(x-\mu)^{2}}{n}$
- **标准差**:描述**典型值和均值距离**;公式:$\sqrt{\text { 方差 }}$
方差的计算使用了数据集的所有数值,而不只是个别极值(如极大值和极小值),因此方差可以很好的反映数据的整体离散程度。
从公式理解,方差是数据偏离平均值距离的平方的平均值。可为什么是偏离平均值距离的平方的平均值,而不是偏离平均值距离的平均值呢?直觉上后者更容易理解才对。
完全正确,**因此就有了标准差**,对方差取平方根就得到了标准差,它同样反映数据的离散程度,但因为它跟原始数据为同一个量纲,更加符合我们的直觉,也更方便解释。
例如一个班的成绩服从正态分布$N(60, 10^2)$,$10^2$=100 是方差,你怎么来描述这个班的成绩情况,这样描述:
这个班的平均成绩是60分,全班同学的成绩与60分差的平方的均值为100
这有点“脱裤放屁”之嫌!!!
引入标准差10之后就可以这样描述了:
这个班的平均成绩是60分,全班同学的成绩与60的平均差距在10分左右。
- **标准分**:对**不同数据集中的数据进行比较**的一种方法;比如:比较两位球员**相对于他们本人**的历史记录的表现。
计算公式: $Z=\frac{x-\mu}{\sigma}$ ($\sigma$为标准差,$\mu$为平均值)
通过上面公式,标准分也可以解释为**距离均值的标准差个数**;
# 第四章 概率计算
**事件**:有概率可言的一个结果或一件事。
**概率空间**(样本空间):表示所有可能的结果。
## 4.1 相关事件
>**相交事件**:$P(A \cup B)=P(A)+P(B)-P(A B)$
**互斥事件**:$P(A \cup B)=P(A)+P(B) ; P(A B)=0$
>**基本条件概率公式**:以事件B为已知的条件的事件A的概率:$P(A \mid B)=\frac{P(A \cap B)}{P(B)}$
>
>注: $P(B) * P(A \mid B)=P(A B)$ -> 即 B发生 + B发生时A发生=A和B都已经发生
>**全概率公式**:$P(B)=\sum_{i=1}^{n} P\left(A_{i}\right) P\left(B \mid A_{i}\right)$
>- 根据条件概率计算一个特定时间的全概率:
>- 其中A1,A2…互不相容,且组成一个样本空间
>**逆概公式**(贝叶斯公式)
>- 在需要求出条件概率,且该条件概率与已知条件概率顺序相反时使用;
>- 基本条件概率公式和全概率公式的组合;
>- 计算逆条件概率:$P(A \mid B)=\frac{P(A) * P(B \mid A)}{P(B)}=\frac{P(A) * P(B \mid A)}{P(A) * P(B \mid A)+P\left(A^{\prime}\right) * P\left(B \mid A^{\prime}\right)}$
## 4.2 独立事件(不相关)
>- 几个事件互不影响,比如放回抽样属于独立事件,不放回抽样属于相关事件。
>- $P(A \mid B)=P(A)$
>- $P(A \cap B)=P(A) * P(B)$
# 第五章 离散概率分布的应用
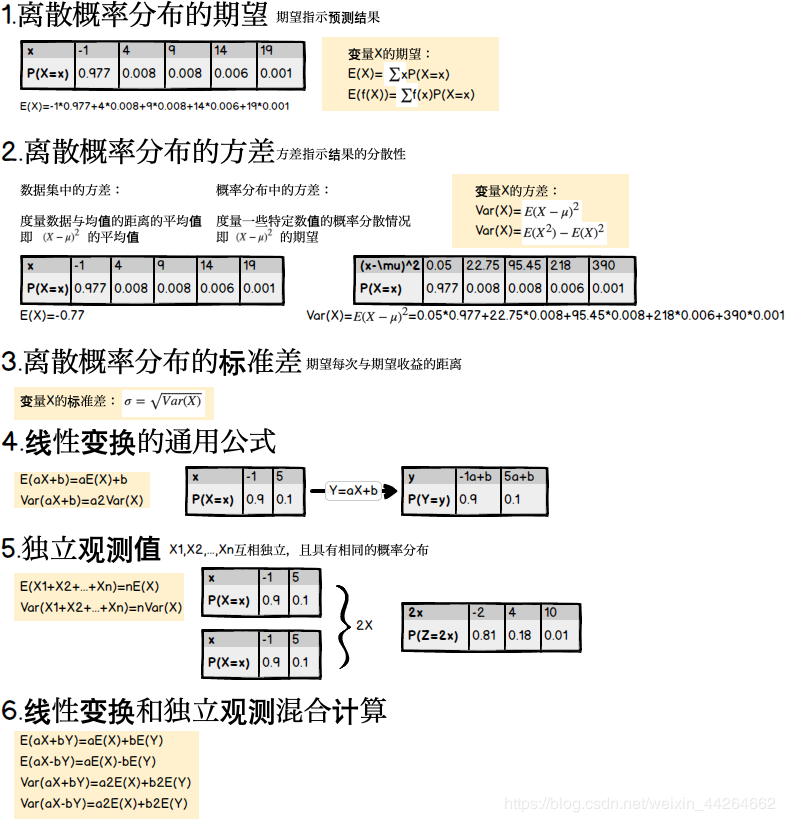
# 第六章 排列与组合
本章内容主要介绍了两个基本概念,**排序与组合**
其中**组合是之后计算二项分布的预备知识**
对于计算而言,重点在于理解其所适应的不同情况,并记忆公式。
## 6.1 排位
**排位方式**:如果要求n个对象的可能排位方式的数目,则:n!=n\*(n-1)\*(n-2)\*…\*3\*2\*1
**按类型排位**:如果要为n个对象排位,其中包括第一类对象k个,第二类对象j个,第三类对象m个.....则排位方式数目的计算式为: $\frac{n !}{k ! j ! m ! \ldots}$
>4匹马,3只骆驼,2只羊比赛,想知道3种动物类型比赛的结果排列有几种:$\frac{7 !}{4 ! 3 ! 2 !}$ , 除去动物内部排列,将其视为一个动物
**取数排位**:一般说来,从n个对象中取出r个对象的排列数目即n个对象中的每一组对象(r个)的可能排位方式数目,通常写作 $^{n} P_{r},$ 即 $:{ }^{n} P_{r}=\frac{n !}{(n-r) !}$
>10匹马,前三名有几个组合方式:$10 * 9 * 8=\frac{10 * 8 * 7 * \ldots 2 * 1}{7 * 6 * \ldots 2 * 1}$
## 6.2 组合
一般说来,组合数目即为从 n 个对象中选取 r 个对象的选取方式的数目,这时不必知道所选对象的确切顺序。组合数目写作 $^{n} C_{r},$ 即: ${ }^{n} C_{r}=\frac{n !}{r !(n-r) !}$
## 6.3 两者区别:
1. 排列与顺序有关
2. 组合与顺序无关