常见概率分布
::: hljs-center
:::
# 第七章 几何分布、二项分布和松柏分布
## 7.1 几何分布:
$X \sim {Geo}({p})$ **应用条件**:
>1. 进行一系列次数有限的独立实验
>1. 每次试验或成功或失败,每次试验的成功概率相同
>1. 主要想知道:**为了取得第一次成功需要试验第多少次**
**p为成功概率,q=1-p为失败概率**
>$P(X=r)=q^{r-1} \cdot p$
>$P(X>r)=q^{r}$
>$P\left(X^{*} \leq r\right)=1-q^{r}$
**期望与方差**:$E(X)=\frac{1}{p}, \quad {Var}(X)=\frac{q}{p^{2}}$
## 7.2 二项分布:
$X \sim B(n, p)$ **应用条件** :
>1. 各观察单位只能具有**相互对立**的一种结果,如阳性或阴性,生存或死亡等,属于两分类资料。
>1. 已知发生某一结果(阳性)的概率为p,其对立结果的概率为1-p,实际工作中要求p是从大量观察中获得**比较稳定的数值**。
>1. n次试验在相同条件下进行,且各个观察单位的观察**结果相互独立**,即每个观察单位的观察结果不会影响到其他观察单位的结果。如要求疾病无传染性、无家族性等。
>1. 主要想知道:**n次试验中成功X次的概率**
${P}({X}={r})={ }^{n} {C}_{r} \cdot {p}^{r} \cdot {q}^{n-r}$
期望与方差:$E(X)=\frac{1}{p}, \quad {Var}(X)=\frac{q}{p^{2}}$
## 7.3 泊松分布:
${X}\sim{Po}({\lambda})$ **应用条件**:
>1. 单个事件在给定区间内随机、独立地发生
>1. 已知给定区间的事件平均发生次数 ${\lambda}$ ,或者叫发生率${\lambda}$
>1. 这个发生次数或发生率是有限的
>1. 主要想知道:**给定区间内的事件发生r次的概率**
${P}\left({X}={r}\right)=\frac{{e}^{-{\lambda}}{\lambda}^{r}}{{r}!}$
**期望与方差**:${E}\left({X}\right)={\lambda}$ , ${Var}\left({X}\right)={\lambda}$
- 如果X和Y是独立随机变量,且都符合泊松分布,则:${X}+{Y}\sim{Po}\left({\lambda}_{X}+{\lambda}_{Y}\right)$
- 如果${X}\sim{B}({n},{p})$,其中n足够大(n>50)且p足够小(p<0.1),则可将该分布近似看作${X}\sim{Po}({np})$ (q足够接近1时${\lambda}$近似np,${\lambda}$近似npq;n足够大时,np更加近似npq,差距相对于本体的大小已经不大了)
>**例子**:你的任务是假装自己是爆米花机,并说出你在下一周的一个特定时间段内发生故障a次的概率。记住,你发生损坏的平均次数是每周3.4次。
>
>**解**:让我们用X代表爆米花机在一周内的故障次数,已知${X}\sim{Po}\left({3}.{4}\right)$,则可知
${P}\left({X}={b}\right)=\frac{{e}^{-{3}.{4}}{{3}.{4}}^{b}}{{b}!}$
注:同分布必然有相同的期望和方差,但反之则不必然;文中所述应是特例
# 第八章 正态分布的应用
**连续型概率分布以及概率密度函数**
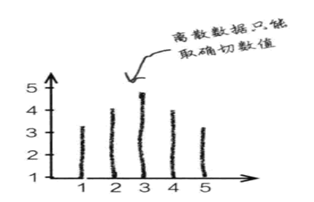
**离散数据**:离散数据由单个数值组成。
::: hljs-center
:::
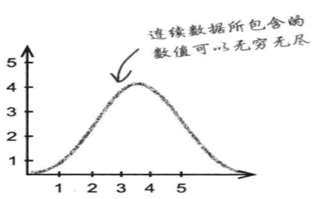
**连续数据**:
连续数据包含一个数据范围,这个范围内的任何一个数值都有可能发生。其数据常常用测量方法得到,而不是用计数方法得到。
::: hljs-center
:::
**连续数据 - 连续概率分布**
>- 连续概率分布可以用概率密度函数进行描述。
>- 通过计算一个数值范围内的概率密度函数下方的面积,可得出该数值范围的概率。也就是说,为了求出$P(a<X<b)$,必须计算a和b之间的概率密度函数下方的面积。
>- 概率密度函数下方的总面积必须等于1。
>- 期望为$\ E(X)=\int{xf(x)\ df}$ , 方差为:$Var(X)=\int{x^2f(x)\ df}-\ E^2(X)$
**连续数据 – 均匀分布**
$f\left(x\right)=\frac{1}{b-a}$ ; $E(X)=\frac{a+b}{2}$ ; $\ Var(X)=\frac{{(b-a)}^2}{12}$
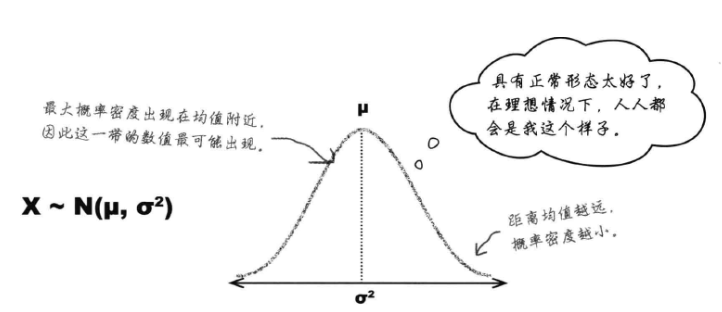
**正态分布(连续数据的理想模型):**
$X\sim N\left(\mu,\sigma^2\right)$ , 均值为${\mu}$、标准差为${\sigma}$。
::: hljs-center
:::
正态分布通过参数$\mu$和$\sigma^2$进行定义,$\mu$指出曲线的中央位置,$\sigma$指出分散性。
::: hljs-center
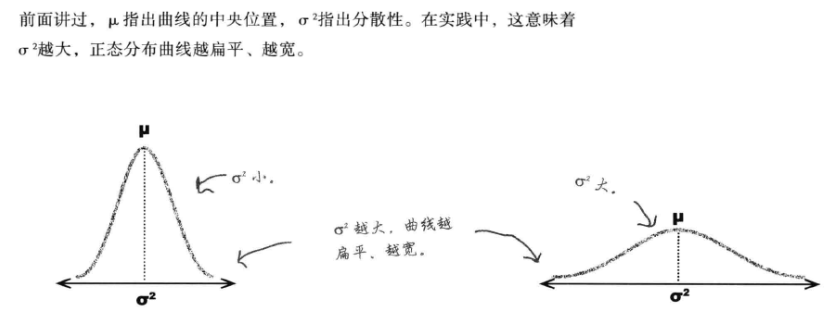
:::
**正态概率计算:**
1. **确定分布**:即找到两个参数的值$\mu$,$\sigma^2$。
1. **使其标准化**:根据步骤(1)把正态分布转化成形式:$Z~N(0,1)$ ,即求Z;目的更好地计算概率,即:利用标准分:$Z=\frac{X-\mu}{\sigma}$ ,将$X\sim N\left(\mu,\sigma^2\right)$变为$Z~N(0,1)$。
1. **使用概率表查找概率**(左侧面积):使用上式**求得出原始数据的标准分后**,查找概率表:
::: hljs-center
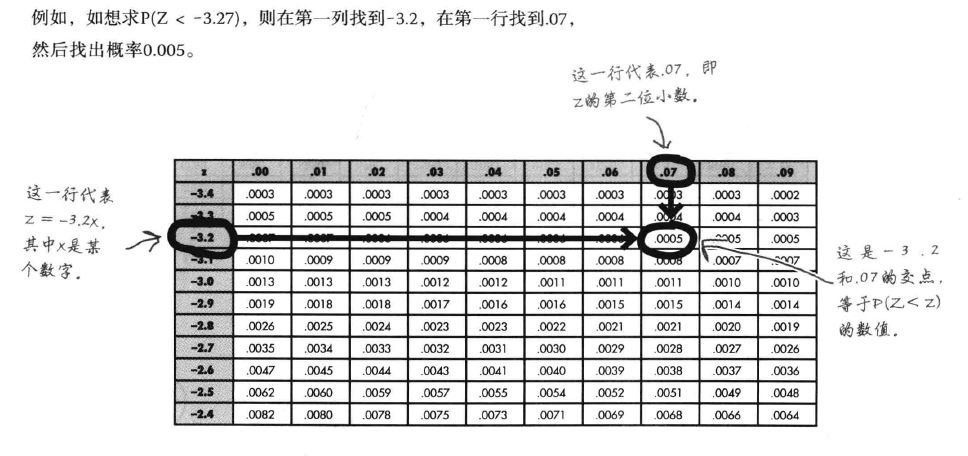
:::
而若求${P}\left({Z}>{a}\right)={1}-{P}\left({Z}<{a}\right) ,\ {P}({a}<{Z}<{b})={P}({Z}<{b})\ -\ {P}({Z}<{a})$
# 第九章 超越正态分布
## 9.1 正态分布间的计算
(注:运用到之前的独立变量,线性变化,独立观测结果的公式)
**随机独立分布**的正态分布:
::: hljs-center

:::
::: hljs-center

:::
**线性变换**的正态分布:$a x+b \sim N\left(a \mu+b, a^{2} \sigma^{2}\right)$
**独立观测值**的正态分布:${x}_{1}+{x}_{2}+\ldots+{x}_{n} \sim {N}\left({n} {\mu}, {n} {\sigma}^{2}\right)$
## 9.2 经验法则(适用于符合正态分布的任何数据集)
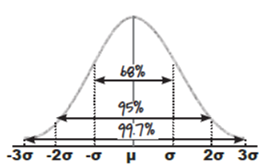
几乎所有的数据都位于**距离均值三个标准差的范围内**
- 大约68%的数值位于距离均值1个标准差的范围内
- 大约95%的数值位于距离均值2个标准差的范围内
- 大约99.7%的数值位于距离均值3个标准差的范围内
::: hljs-center
:::
## 9.3 二项分布的近似
::: hljs-center
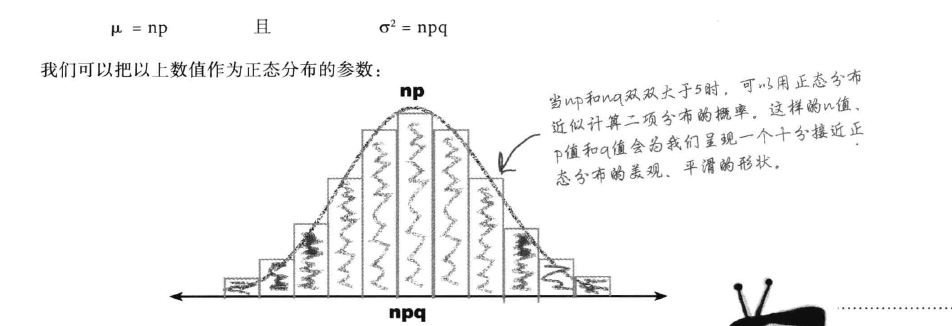
:::
**连续性修正:**
二项分布的变量是离散的,而正态分布的变量是连续的。故要做连续性修正,具体如下:
::: hljs-center

:::
## 9.4 泊松分布的近似
如果$x \sim {Po}(\lambda)$ 且 $\lambda>15$,则可用$x \sim N(\lambda, \lambda)$进行近似。**不过需要进行连续性修正**
**小结**:**正态分布是最典型的一种连续型分布**,这个世界中的大多数事情都符合正态分布,在合适的条件下,还能使用正态分布近似二项分布和泊松分布,**不要忘了进行连续性修正**。