概率统计应用
::: hljs-center
:::
# 第十章 统计抽样的运用:抽取样本
>**统计需要处理数据,数据从何而来?**
有时候收集数据很简单,有时候收集数据很复杂。
在实际工作中,如何成功地收集数据——有效地,正确地,省时省钱地收集数据?
**抽样是一种很好的方法。**
>**总体**
统计学上的总体指的是准备对其进行测量、研究或者分析的整个群体,可以是人、得分,也可以是糖果——关键在于总体指的是所有的对象。
>**普查**
指的是对总体进行研究和调查。
普查可以给出总体的准确信息,但并不是在任何情况下都切实可行。当总体数量很大时,或者说无穷大时,就不可能对每一个对象进行研究了。若是这样,既费时又费力,关键是很大程度不一定可行。
>**样本**
统计学上的样本是指从总体中选取一部分对象。通过选取样本,使其恰当的代表总体,从而得到代表总体的一个子集。
仅对总体的一个样本进行调查或者研究称为样本调查。在多数情况下,样本调查比普查更切实可行,且不用考虑整个总体。
>**抽样方法**
建立一个好样本的关键是尽量选取最符合总体的样本,如果样本具有代表性,则表示样本具有与总体十分相似的特性,进而意味着可以通过样本预测出总体具有那种特征。
使用错误的样本会对总体参数(比方说期望和标准差)得出错误的结论,你可能会对数据形成截然不同的观点,进而做出错误的决策。
>**如何设计样本?**
样本的作用是用来判定总体情况。为了确保得到正确的结果,需要明智地选择样本。
>1. **确定目标总体**
目标总体指你正在研究的,并且打算为其采集结果的群体。
目标总体要尽可能精确。
>1. **确定抽样单位**
明确目标总体后,就需要决定要抽取哪一类对象。
>1. **确定抽样空间**
抽样空间是这样一张表,表中列出目标总体范围内的所有抽样单位,最好给每个抽样单位取个名或者编个号。基本上,你可以从抽样空间里进行抽样。
>**偏倚**
**样本有时会发生偏倚**
你在无意间或者有意间带入样本的某种个人偏好就是偏倚,这时,你的样本不再是从总体中进行随机选择的结果。
**如果一个样本无偏,则这个样本可以代表总体,是总体的客观反映。**
>**偏倚产生的一些原因**
>- 抽样空间中条目不齐全,因此未包含目标总体中的所有对象
>- 抽样单位不正确
>- 为样本选取的一个个抽样单位没有出现在实际样本中
>- 调查问卷设计不当
>- 样本缺乏随机性
>
>如上所述,偏倚来源广泛,而其中大部分归咎于样本选取方法。我们需要采用合适的样本选取方法,使得偏倚发生几率降至最低程度。
>**如何选取样本?**
>1.**简单随机抽样**
>- 重复抽样
重复抽样指的是:在选取一个抽样单位并记录下这个抽样单位的相关信息之后,再将这个单位放回总体中。这样操作的结果是某个抽样单位有可能被选取不止一次。
>- 不重复抽样
不重复抽样指的是:不再将抽样单位放回总体中。
>
>使用简单随机抽样的主要两种方法:抽签或者使用随机编号。
>使用简单随机抽样时,仍然存在样本无法代表总体的可能性。
>
>2.**分层抽样**
>分层抽样是指将总体分割为几个相似的组,每个组具有相似的类型。这些特性或者组称为分层。分好层后,就可以对每一层进行简单随机抽样,确保最终样本中具有每一个组的代表。
>
>3.**整群抽样**
进行整群抽样,不是对抽样单位进行简单随机抽样,而是对群进行简单随机抽样。
>
>4.**系统抽样**
使用系统抽样时,按着某种顺序列出总体名单,然后每k个单位进行一次调查,其中k为一个特定的数字。
# 第十一章 总体和样本的估计:进行预测
**得样本而知总体,不亦乐乎。通过样本去推知总体,属于推断性统计学。**
若要想成为样本专家,首先需要有效地利用样本去准确地预测总体,并以一定方式说明预测结果的可靠程度。
## 11.1 点估计量(样本 -> 总体)
样本均值被称为总体均值的点估计量,换而言之,样本均值,作为一个对于所有样本数据的计算结果,它是总体均值的良好估计。
**1.点估计量近似总体参数**
当总体参数的确切数值无法获知的情况下,我们用“点估计量”对总体参数进行最接近的猜测。
一个总体参数的点估计量是指用于估计总体参数数值的某个函数或者算式。例如样本均值是总体均值的点估计量。
- 估计总体均值:$\hat{\mu}=\bar{x}=\frac{\sum x}{n}$ ;[ $\mu$是总体均值,$\bar{x}$是样本均值,$\hat{\mu}$是$\mu$的点估计量 ]
- 估计总体方差:${\hat{\sigma}}^2=S^2=\frac{\sum{(x-\bar{x})}^2}{n-1}$ ;[ $\sigma^2$是总体方差,$S^2$是样本方差,${\hat{\sigma}}^2$是$\sigma^2$的点估计量] (n-1是因为总体方差往往大于样本方差)
- 估计总体比例:$\hat{p}=p_s$=成功数目样本数目 ;[ $p$是总体成功的比例,$p_s$是样本成功比例,$\hat{p}$是$p$的点估计量]
## 11.2 (不重复)抽样分布(总体 -> 样本)
- **1. 比例的抽样分布总结**
利用比例的抽样分布,能够求出某一个随机选择的、大小为n的样本的“成功比例”的概率。
>**例如**:
每一大盒糖球的容量为100颗,我们需要求出在一大盒特定糖球(样本)中红色糖球占40%的概率,且已知糖球总体的25%是红色的。
也就是说,我们能够利用比例的抽样分布求出“某一大盒糖球中的红色糖球比例至少为40%”的概率。
**不过,在此之前,我们需要知道上述分布的期望和方差**。
以上例为例,样本中的红色糖球的比例取决于$X$:样本中的红色糖球的数目,即比例本身是一个随机变量,可以将此记为$p_s$,且 $p_s=\ X/n$。
即 ${p}_{s}$ 代表样本比例随机变量,因此比例的抽样分布总结又可称为$p_s$的抽样分布
由例有:${X}\sim{B}(n,p)$,则${E}\left({X}\right)={np}$,${Var}\left({X}\right)={npq}$
**期望与方差**:
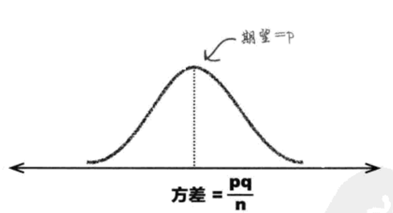
${E}\left({p}_{s}\right)={E}\left(\frac{{X}}{{n}}\right)=\frac{{E}\left({X}\right)}{{n}}=\frac{{np}}{{n}}={p}$ ;
${Var}\left({p}_{s}\right)=\frac{{Var}\left({X}\right)}{{n}^{2}}=\frac{{npq}}{{n}^{2}}=\frac{{pq}}{{n}}$ ;
标准差=$\sqrt{{Var}\left({p}_{s}\right)}$ [ p为总体比例(成功概率),q为1-p ]
因此若n>30,则符合正态分布 ${p}_{s}={N} \sim\left({p}, \frac{p {q}}{n}\right)$
::: hljs-center
:::
- **1.11 连续性修正:**
连续性修正= $\frac{\pm(1 / 2)}{n}=\frac{\pm 1}{2 n}$ ,如果n很大可以忽略连续性修正
即,如果用正态分布近似计算P。的概率,一定要用$\pm(1 / 2)$进行连续性修正;连续性修正的确切数值取决于数值n。
---
- **2. 均值的抽样分布总结**
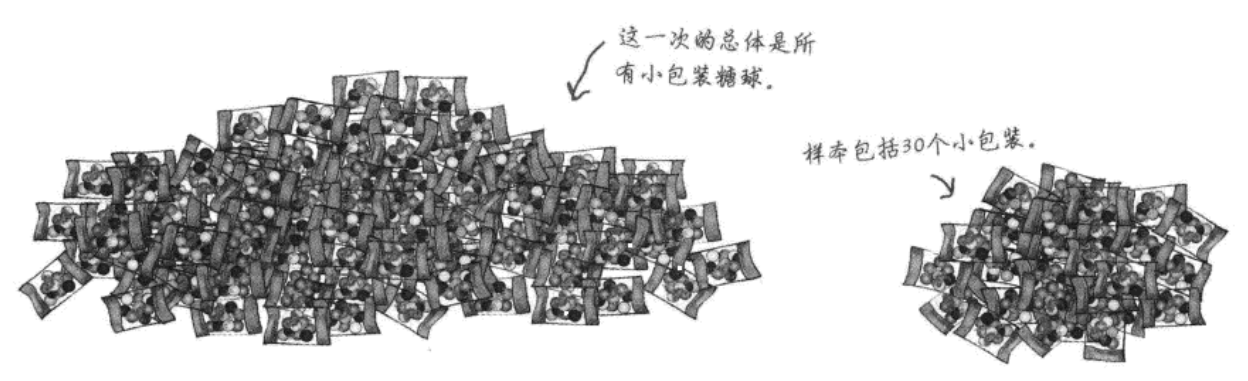
这个问题与前面的问题略有不同。我们已知小包装糖球的总体均值和方差,然后抽取了几袋糖球作为样本,需要为该样本计算概率。这一次,我们不需要计算样本比例的概率,而要计算样本均值的概率。
::: hljs-center
:::
- 均值的抽样分布为我们提供了一种计算样本均值的概率的方法。为了计算任何一个变量的概率,先要知道这个变量的概率分布,所以,**若要计算样本均值的概率,就需要知道样本均值的分布。**
>- **我们的例子**是这样的:在一个有30袋糖球的样本中,求糖球数目的均值小于或等于8.5的概率。和比例的抽样分布一样,为了能够动手计算概率,先要知道分布的期望和方差。
>
>- $\bar{{X}}=\frac{{X}_{1}+{X}_{2}.+..+{X}_{n}}{{n}}$ ; 根据:${E}\left({ax}\right)={aE}$(${x}$) ;$E(X+Y)=E(X)+E(Y)$
得到**期望与方差**:$E(\bar{X})=E\left(\frac{X_{1}+X_{2} \cdot t_{n}+X_{n}}{n}\right)=\frac{1}{n}\left(E\left(x_{1}\right)+E\left(x_{2}\right)+\ldots+E\left(x_{n}\right)\right)$
每个$X_i$,都是$X$的一个独立观察结果,于是它们遵守相同的分布;每一个$X$的期望都是$\mu$,方差都是$\sigma^2$。则:$E(\bar{X})=\frac{1}{n}\left(E\left(x_{1}\right)+E\left(x_{2}\right)+\ldots+E\left(x_{n}\right)\right) \mid=\frac{1}{n}(\mu+\mu+\ldots+\mu)=\mu$
>
>- **方差**: ${Var}(\bar{X})={Var}\left(\frac{X_{1}+X_{2}+\ldots+X_{n}}{n}\right)={Var}\left(\frac{X_{1}}{n}+\frac{X_{2}}{n}+\ldots+\frac{X_{n}}{n}\right)=\left(\frac{1}{n}\right)^{2}\left({Var}\left(x_{1}\right)+\right.$
$\left.{Var}\left(x_{1}\right)+\ldots+{Var}\left(x_{n}\right)\right)=\frac{1}{n^{2}}\left(\sigma^{2}+\sigma^{2}+\ldots+\sigma^{2}\right)=\frac{\sigma^{2}}{n}$
>
>- **$\bar{X}$的分布不同于$X$的分布**
>
>- **标准差**:$\sqrt{Var\left(\bar{X}\right)}$
>
>- $\bar{{X}}$的分布:如果${X}\sim{N}\left({\mu},{\sigma}^{2}\right)$ ,则$\bar{{X}}\sim{N}\left({\mu},{\sigma}^{2}/{n}\right)$
**中心极限定理**:如果如果n很大(>30)但X不符合正态分布则$\bar{{X}}\sim{N}\left({\mu},{\sigma}^{2}/{n}\right)$ [ 此处方差期望是$\bar{{X}}$的 ]
::: hljs-center

:::
在**重置抽样**时,样本均值的方差为总体方 $\sigma^{2}$ 的1/n, 即 $\frac{\sigma^{2}}{n}$
在**不重置抽样**时,样本均值的方差为 $\sigma_{\bar{x}}^{2}=\frac{\sigma^{2}}{n} \frac{N-n}{N-1}$
# 第十二章 置信区间的构建
我们的确可以使用点估计量来估计总体均值、方差或一定比例的精确值,但是我们始终无法确定我们使用的样本一定是无偏样本,因此我们考虑使用置信区间的方法来估计总体统计量,因为它是考虑了不确定性的方法。
## 12.1 具体内容
糖果公司用一个包含100粒糖球的样本得出口味持续时间均值的点估计量为62.7分钟,于是便在电视节目黄金时段宣布其公司糖球口味的平均持续时间为62.7分钟,但有人自行做了测试,得出了不同的结果,威胁要起诉糖果公司。
此时,我们应该制定的是总体均值的估计值的区间范围,而不是一个精确值,因为这样的话会给予我们更大的误差空间,就不容易被人起诉了。
## 12.2 求解置信区间的步骤
1. **选择总体统计量**
在问题中,需要为糖球口味持续时间的均值来构建区间,于是需要为总体均值$\mu$来构建一个置信区间。
1. **求出其抽样分布**
**为了求出总体均值的抽样分布,我们需要直到均值的抽样分布**。我们需要先计算出 $\bar{X}$ 的期望、方差和分布。而这些在上一节中已经计算过了。$E(\bar{X})=\mu$ , $Var(\bar{X})=\frac{\sigma^2}{n}$ ;为了利用以上结果求出$\mu$的置信区间,我们带入总体方差的数值$\sigma^2$和样本大小的数值n ;
此时一个问题是我们现在并不知道总体的方差是多少,但是我们可以借用**点估计法** $\hat{\mu}$或$s^2$来近似替代,因为这已经是我们目前所具有的数据中可以得到的最近似的值了。公式进一步推导成如下形式:$E(\bar{X})=\mu$ , $Var(\bar{X})=\frac{s^2}{n}$ [ 这是方差的点估计量,我们不知道总体方差的真实值是多少,于是用样本方差进行估计 ]
对于样本均值的分布,我们可以根据 "若$X$符合正态分布,那么$\bar{X}$也符合正态分布" 的定理来得知,其应符合正态分布。在本题中即是 $\bar{X} \sim N\left(\mu, \frac{s^{2}}{n}\right)$ 。
1. **决定置信水平**
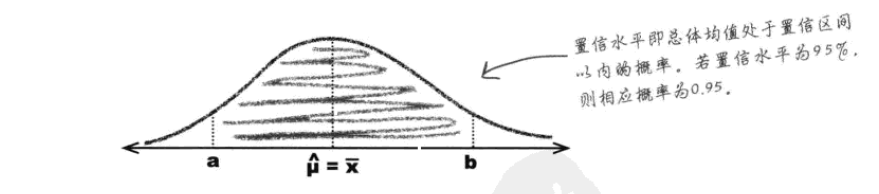
置信水平表明你希望自己对于“总体统计量落入置信区间”的这一说法有多大的把握,比如我们希望总体均值的执行水平为95%,这表明总体均值处于置信区间的概率为0.95,当然可以更高如99%,这样糖果公司就可以更有信心在广告宣称“总体均值位于这个置信区间”这一说法。
值得注意的是,置信水平越高,区间越宽,也就是确定的概率越大,范围越广,也越对说法有把握。
为了防止说法几乎毫无意义,我们需要确定一个合适的置信水平,确保范围小而可靠,对此,我们一般采用95%作为常用置信水平。
::: hljs-center
:::
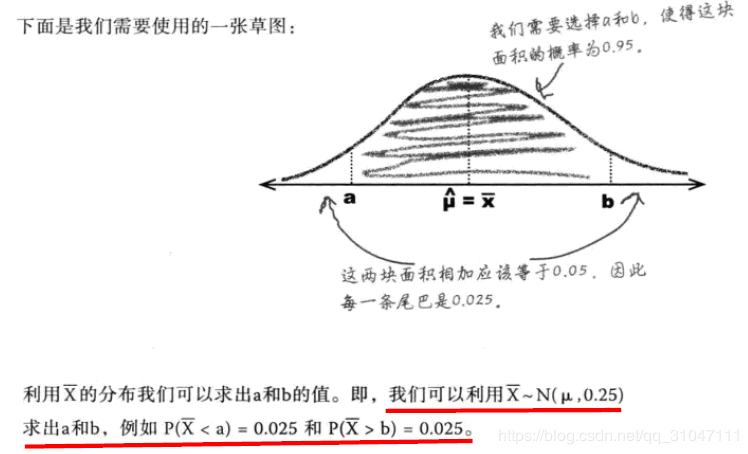
4. **求出置信上下限**
根据抽样分布和选择好的置信水平来求出置信上下限,从而确定置信区间的范围。
::: hljs-center
:::
- 此时我们再将$\bar{X}$进行标准化 [$Z=\frac{X-\mu}{\sigma}$] ,从而利用正态分布表来查出其对应的区间值。
::: hljs-center
$P(-1.96<\frac{\bar{X}-\mu}{0.5}<1.96)=0.95$
:::
- 此时我们将括号里面的不等式进行展开,即可确定置信区间范围,其中$\bar{X}$可以通过样本$\bar{x}$ 来计算。
::: hljs-center

:::
- 得出最后结果:祝贺!你旗开得胜,求出了一个置信区间。你的结论是:区间(61.72,63.68)中包含糖球口味持续时间总体均值的几率是95%。
## 12.3 例子


## 12.4 置信区间的简便算法
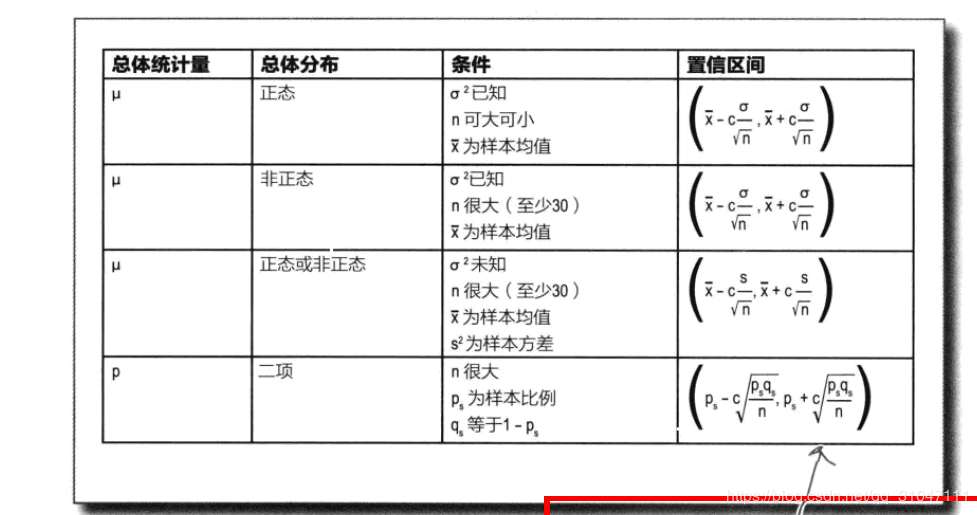
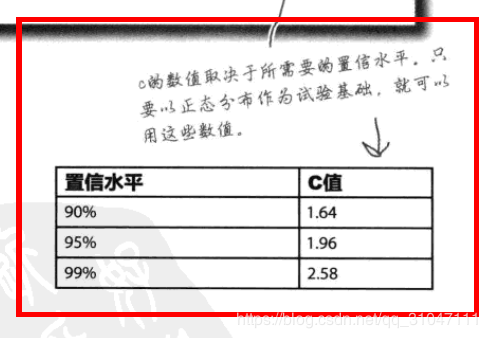
- **统计量的抽样分布符合正态分布时**
::: hljs-center
:::
::: hljs-center
:::
- **统计量的抽样分布符合T分布时**
::: hljs-center

:::
- **特殊情况 —— 总体正态、样本T分布**
并非任何情况都能用正态分布进行良好近似。我们前面讲过的所有抽样分布要么符合正态分布,要么可以用正态分布进行近似。问题是,我们无法对每一个置信区间都使用正态分布。不巧,目前碰上的就是这种不能用正态分布的情况。不能用正态分布的原因何在?当抽样很大时,正态分布是求解置信区间的理想分布-能得出精确结果,且与总体本身是否是正态分布无关。现在我们碰到了另一种情况:尽管$X$本身符合正态分布,$\bar{{X}}$却并不符合。
>糖果公司想求出糖球重量的置信区间,但只抽取了少量的样本,比如抽取了一个具有代表性的样本,共10颗,然后称了每一粒糖球的重量,计算出这个样本的 $\bar{X}=0.5$,$s^2=0.09$,此时该如何求出其置信区间。
>1. **选择总体统计量**
我们需要为糖球重量均值构建一个置信区间,也就是要为总体均值\mu构建置信区间。
>1. **求$\bar{{X}}$的概率分布**
当总体符合正态分布,${\delta}^{2}$未知,且可供支配的样本很小时,$\bar{{X}}$符合T分布。而当样本数量为n个时,T分布的形式为$T\sim t(n-1)$,而$T=\frac{\bar{X}-\mu}{s/\sqrt n}$ ,也就是说在这道题中$T=\frac{\bar{X}-\mu}{s / \sqrt{n}} \sim \mathrm{t}(9)$ 。
>
>::: hljs-center
>
>
>
>:::
>
>
> 3. **决定置信水平: 一般设置为95%**
>
>4. **求出${\mu}$的置信上下限**
>::: hljs-center
>
>
>
>:::
>- 再利用T分布概率表可求出P(T>t)=p中的t值,在这道题中p=0.025
>
>::: hljs-center
>
>
>
>:::
# 第十三章 假设检验的运用:研究证据
>**假设检验的步骤**
>- 确定要进行检验的假设
>- 选择检验统计量
>- 确定用于做决策的拒绝域
>- 求出检验统计的p值
>- 查看样本结果是否位于拒绝域
>- 做出决策
示例:统计邦头号制药公司生产了一-种治疗打鼾的新药物。被打呼噜折磨不堪的患者纷纷赶往医院,指望能得到睡眠救星。制药公司断言他们的神药能在两周内治愈90%的患者,对于深受打鼾困扰的人来说,这可是个天大的好消息。问题是,并非人人都信服这个断言。统计邦外科诊所的医生给病人开了鼾克,但她对结果感到失望。她决定自行对药物进行试验。她随机抽取了15位鼻鼾患者,对这些患者实施为期2周的鼾克疗法。两周后,她请这些患者来医院复诊,看他们是否不再打鼾。结果如下:
|是否治愈?|是|否|
|-|-|-|
|频数|11|4|
**step1:确定假设**
与原假设对立的断言被称为备择假设,用$H_1$表示。如果有足够的证据拒绝$H_0$,我们就接受$H_1$
我们所检验的这个断言被称为原假设,以$H_0$表示,除非我们有充分证据进行反驳,否则就要接受这个断言。
进行假设检验时,你假定原假设为真;如果有足够的证据反驳原假设,则拒绝原假设,接受备择假设。
在此例中$H_0$:P=90% ; $H_1$:P<90%
**step2:选择检验统计量**
借助检验统计量,用于对假设进行检验的统计量是与该检验关系最为密切的统计量。
如果用X表示样本人数,就可以将X作为检验统计量。样本中共有15名患者,根据制药公司的说法,成功概率为0.9。由于X符合二项分布,于是检验统计量实际上符合:X~B(15,0.9)
**step3: 确定拒绝域**
拒绝域是一组数值,这组数值给出了反驳原假设最极端的证据。针对本例中,如果治愈的人数在90%以上则与制药公司的断言相符合,否则就是对立假设如果治疗痊愈的人数在拒绝域内,我们就说有足够的证据可以反驳原假设,但是如果在拒绝域外,我们就得承认没有足够的证据可以反驳原假设,我们把拒绝域的分界点成为“c”。
为求拒绝域,先定显著性水平,假设我们以5%为显著水平检验制药公司的断言,治愈人数小于c的概率小于5%
即:如果我们用X表示治愈的鼻鼾患者的数目,则我们将拒绝域定义为能令下列不等式成立的一些数值:$P(X<c)<\alpha$ ,其中 $\alpha$=5%
**显著性水平用${a}$表示。它表明你希望在观察结果的不可能程度达到多大时拒绝${H}_{0}$**
>**需要明确构建的是单尾检验还是双尾检验**
>- **单尾检验**
>**拒绝域落在可能的数据集的一侧**
单尾检验即检验的拒绝域落在可能的数据集的一侧,你选择检验水平----以$\alpha$表示,然后确保拒绝域以相应的概率反映这个水平。尾部可以是可能数据集的左侧或右侧,具体用哪一侧取决于备择假设$H_1$。如果备择假设包含一个<符号,则使用左尾,此时拒绝域位于数据的低端。如果备择假设包含一个>符号,则使用右尾,此时拒绝域位于数据的高端。我们对鼻鼾克使用的是单尾检验,由于备择假设为$p<0.9$,因此拒绝域位于左尾。
>
>- **双尾检验**
双尾检验即**拒绝域一分为二位于数据集的两侧**,你选择检验水平$\alpha$,然后将拒绝域一分为二,并确保整个拒绝域以相应概率反映这个检验水平。两侧各占$\alpha/2$,因此总和为a。
**step 4:求出p值**
**p值**:即某个小于或者等于拒绝域方向上的一个样本的概率。具体求法是利用样本进行计算,然后判断样本的结果是否落在拒绝域以内。
假设参与治愈的人数为11人,而拒绝域分布在低端,于是P(X<=11)小于0.05,则说明11落在拒绝域中,这样我们就可以拒绝原假设了
::: hljs-center

:::
**step 5:样本结果位于拒绝域中吗**
因为p=0.055大于0.05,不在拒绝域中
**step 6:做出决策**
因为假设检验的p值落在检验的拒绝域以外,所以没有充分的证据证明拒绝原假设。所以,我们接受了制药公司的断言。
>**当我们扩展样本的数量新数据的样子如下**
>|是否治愈?|是|否|
>|-|-|-|
>|频数|80|20|
>
>**重复**上述的过程,这里面**忽略了相同的步骤**
>
>**step2:选择统计量**
>因为这次的样本个数为100人,符合二项分布B(100,0.9)这里书中使用了用正态分布近似替代二项分布的算法。由于n很大,且np和nq都大于5,我们就用$X~\ N(np,\ npq)$作为检验统计量,其中X为成功治愈的患者的数目。即我们能够用$X~N(90,9)$
>
>**step3:求出拒绝域**
由于我们的显著性水平为5%,于是临界值c等于令P(Z<c)=0.05的数值。在概率表中查找0.05,得到c的数值为 -1.64,即: $P\left(Z<-1.64\right)=0.05$
>
>这里我们可以直接用X来求出x对应的c
>计算标准分Z的值
>::: hljs-center
>
>
>
>:::
>
>**step4: 求p值**,治愈的人数是80人,则P(X<80)的概率为

>
>**step5: 因为p在拒绝域内**
>
>**step6: 做出决策**:原假设不充分,我们采用备用假设。
---
**可能出现的错误**
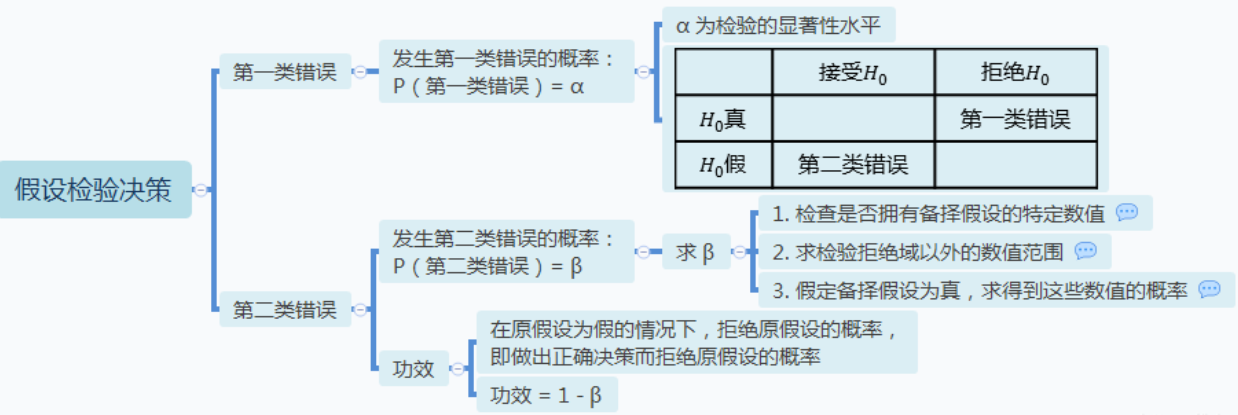
假设检验的基本方法是这样的:选取一个断言,对其进行检验一评估对其不利的证据。如果有足够的不利证据,则否定该断言;如果没有足够的不利证据,则接受该断言。你可能会正确地接受或拒绝原假设,但即使在考虑了证据的情况下,仍然有可能犯错误。你可能会拒绝一个正确的原假设,也可能接受一个实质上错误的原假设。
统计学家为以上类型的错误给出了专用名称。
- **第一类错误**:错误地拒绝真原假设;
- **第二类错误**:错误地接受假原假设。
假设检验的功效即你正确地拒绝一个假原假设的概率,即:
- P(**发生第一类错误**)=α ,其中$\alpha$为检验的显著性水平。
- **发生第二类错误**的概率通常用希腊字母$\beta$表示:P(**发生第二类错误**)=β,计算$\beta$的方法如下:
::: hljs-center

:::
::: hljs-center

:::
只要求出P(发生第二类错误),再计算假设检验的功效就容易了。
在$H_0$为假时拒绝$H_1$,其实就是发生第二类错误的相反情况。即:功效=1-β,其中$\beta$等于发生第二类错误的概率。
下面通过具体的实例来分析
首先我们需要H1:备选假设,这里我们使用医生建议的成功率0.8(**需要注意的是,我们用P=0.8,而不是p<0.8**)
其次我们要求出数据的取值范围:在拒绝域外的X的取值范围P(X<c)>0.05,X的取值为85.06.则治愈人数为85.06或者更多的情况下,我们会接受原假设.
最后,我们需要计算H1为真的概率,**P(X>=85.06),X~N(np,npq)=N(80,16)**
::: hljs-center

:::
>**最后通过一组练习题来复习一下本章的内容:**
制药公司和他们的止咳糖浆制造厂发生了争议,厂方说注入药瓶的糖浆量符合正态分布$X \sim N(355,25)$,其中X是量得的每瓶糖浆容量,单位mL。制药公司用大样本进行了检验,发现100瓶糖浆的平均容量为356.5mL。请以1%的显著性水平检验厂方给出的均值假设,与此相对的另一说法是每瓶糖浆的容量均值大于355mL。
>
>**H0:** 为厂家的说法,糖浆量符合正态分布X~N(355,25)
>**H1:** 每瓶糖浆的容量大于355
>**显著水平为1%**
>**抽样100瓶,均值为356.5ml**
>
>**第1步:确定要进行检验的假设**。原假设是什么?备择假设是什么?
>假设厂家的说法是正确的,那么每瓶药的糖浆为355ml
>备选假设为另外一种说法,每瓶药中的糖浆大于355ml
>
>**第2步:选择检验统计量**
$\overline{\mathrm{X}} \sim \mathrm{N}\left(\mu, \sigma^{2} / \mathrm{n}\right),$ 因此根据原假设得知 $: \bar{X} \sim N(355,25 / 100)$ 或 $\bar{X} \sim N(355,0.25)$
统计量为糖浆的装填量,符合抽样的正态分布
>
>**第3步:决定用于做决策的拒绝域**。拒绝域位于分布的左尾还是右尾?显著性水平是多少?
>因为备选假设为均值大于355ml,所以**拒绝域位于右尾**
>**显著水平**根据题设为0.01
>使用**标准分计算**P(Z<c)>0.01
>c的取值为:
>
>如果使用X去求C

>
>**第4步:求假设检验的p值:**
使用分布$Z\ =\ (X\ -\ 355)/0.5$,即样本糖浆的容量均值,记住,这一次你需要查看检验统计量是否位于分布的右尾,因为这正是拒绝域所在位置。
抽样的结果为100瓶,均值为356.5ml
>**求出P值**
>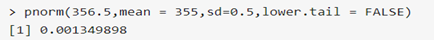
>
>**第5步:查看样本结果是否位于拒绝域以内**。记住:检验的显著性水平是1%。
>p值小于显著水平,在拒绝域内
>另外可以看到抽样值356.5在显著水平对应的X=356.1632外,并且是右尾,**在拒绝域内,拒绝原假设,采用对立的备用假设。**
>
>**第6步:作出决策;** 是否有足够的证据拒绝显著性水平为1 %的原假设?
由于样本结果位于拒绝域以内。有充分的证据拒绝原假设.我们可以**接受备择假设: $\mu\ >\ 355\ ml$**
# 第十四章 χ² 分布:继续探讨
**有时候事实与期望并不相符。**
当以一种特定的概率分布为某种情况建模时,对于事物的长期可能结果,你有十分清晰的想法。可如果期望与事实存在差别呢?你该如何判断? 这些偏差是正常波动,还是说明概率模型存在问题?本章将讲解如何利用χ² 分布分析结果,排除可疑结果。